
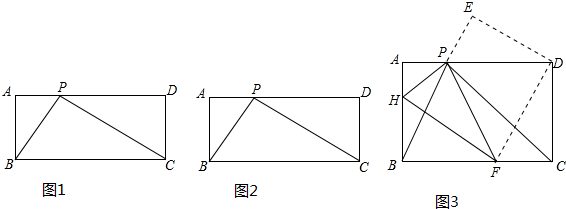
���� ��1���ɡ�ABP�ס�DPC����$\frac{AP}{DC}$=$\frac{AB}{PD}$���ɴ˼��ɽ�����⣮
��2����ͼ2�У�����B����AD�ĶԳƵ�E������CE��AD�ڵ�P����ʱPB+PC��С��PB+PC=PE+PC=EC������֮���߶���̣����ɡ�APE�ա�DPC���õ�PE=PC��
�ٸ��ݵ������������ߺ�һ���ɽ�����⣮
��3����ͼ3�У��ӳ�FP��BA���ӳ�����H������BD��PF�ڵ�O����ʱ|FH-PH|��ֵ�����BF=DF=x����Rt��DFC�У���DF2=CD2+CF2�����x���ɡ�POD�ա�FOB��
�Ƴ�PD=BF=$\frac{25}{4}$������AP��BF����$\frac{AP}{BF}$=$\frac{AH}{AH+AB}$���ɴ˼��ɽ�����⣮
��� �⣺��1����ͼ1�У�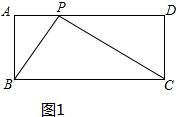
���ı���ABCD�Ǿ��Σ�
���A=��D=90�㣬AB=CD��BC=AD��
�ߡ�BPC=90�㣬
���APB+��DPC=90�㣬�ߡ�ABP+��APB=90�㣬
���ABP=��DPC��
���ABP�ס�DPC��
��$\frac{AP}{DC}$=$\frac{AB}{PD}$��
��CD=AB=3��PD=4��
��$\frac{AP}{3}$=$\frac{3}{4}$��
��AP=$\frac{9}{4}$��
��2����ͼ2�У�����B����AD�ĶԳƵ�E������CE��AD�ڵ�P����ʱPB+PC��С��PB+PC=PE+PC=EC������֮���߶���̣�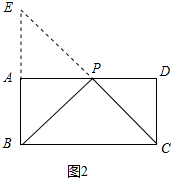
��AB=AE=CD��BC=2AB��AE��CD��
���E=��PCD��BC=BE��
�ڡ�APE�͡�DPC�У�
$\left\{\begin{array}{l}{��APE=��CPD}\\{��E=��PCD}\\{AE=CD}\end{array}\right.$��
���APE�ա�DPC��
��PE=PC����BC=BE��
��BP��CE��
���BPC=90�㣮
��3����ͼ3�У��ӳ�FP��BA���ӳ�����H������BD��PF�ڵ�O��
��ʱ|FH-PH|��ֵ�������FH-PH��PF����H��P��F���㹲��ʱ��FH-PH=PF�����Դ�ʱ|FH-PH|��ֵ���
���ı���PFDE�����ı���PFBA���۵õ���
��OB=OD��BF=DF����BF=DF=x��
��Rt��DFC����DF2=CD2+CF2��
��x2=62+��8-x��2��
��x=$\frac{25}{4}$��
��PD��BF��
���PDB=��FBD��
�ڡ�POD�͡�FOB�У�
$\left\{\begin{array}{l}{��PDO=��FBO}\\{��POD=��BOF}\\{DO=OB}\end{array}\right.$��
���POD�ա�FOB��
��PD=BF=$\frac{25}{4}$��
��AP=AD-PD=8-$\frac{25}{4}$=$\frac{7}{4}$��
��AP��BF��
��$\frac{AP}{BF}$=$\frac{AH}{AH+AB}$��
��$\frac{\frac{7}{4}}{\frac{25}{4}}$=$\frac{AH}{AH+6}$��
��AH=$\frac{7}{3}$��
���� ���⿼���ı����ۺ��⡢���ε����ʡ�ȫ�������ε��ж������ʡ�ƽ���߷��߶γɱ������������ɶ�����֪ʶ������Ĺؼ������������Щ֪ʶ������⡢ѧ�����öԳƽ����Сֵ���⣬��������������֮��С�ڵ����߽�����ֵ���⣬�����п�ѹ���⣮


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | ƽ���ı��� | C�� | ˫���� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25+25=26 | B�� | x3+x3=x6 | C�� | ��2x3��2=4x9 | D�� | ��3x3��2=6x6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-x+5=0 | B�� | x2-x-5=0 | C�� | x2+x+5=0 | D�� | x2+x-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9.2��1010 | B�� | 92.7��108 | C�� | 9.27��109 | D�� | 9.3��109 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com