练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．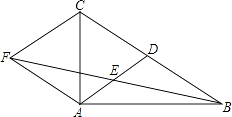
    （1）求证：AF=DC；
    （2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

    【答案】
    （1）证明：∵AF∥BC，

    ∴∠AFE=∠DBE，

    ∵E是AD的中点，AD是BC边上的中线，

    ∴AE=DE，BD=CD，

    在△AFE和△DBE中

    ∴△AFE≌△DBE（AAS），

    ∴AF=BD，

    ∴AF=DC


    （2）四边形ADCF是菱形，

    证明：AF∥BC，AF=DC，

    ∴四边形ADCF是平行四边形，

    ∵AC⊥AB，AD是斜边BC的中线，

    ∴AD= BC=DC，

    ∴平行四边形ADCF是菱形


    【解析】（1）根据AAS证△AFE≌△DBE，推出AF=BD，即可得出答案；（2）得出四边形ADCF是平行四边形，根据直角三角形斜边上中线性质得出CD=AD，根据菱形的判定推出即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】分解因式：3m（2x﹣y）2﹣3mn2= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个多边形的内角和是720°，这个多边形的边数是（ ）
    A.3
    B.4
    C.5
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

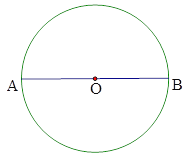
    【题目】如图，AB是⊙O的直径，AB=2.

    （1）尺规作图（保留作图痕迹，不写作法）：作⊙O的内接正六边形ACDBEF。

    （2）在（1）的条件下，直线PE与⊙O相切于点E，交AB延长线于点P，求PB、PE和所围成的图形面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小红同学要测量A、C两地的距离，但A、C之间有一水池，不能直接测量，于是她在A、C同一水平面上选取了一点B，点B可直接到达A、C两地．她测量得到AB=80米，BC=20米，∠ABC=120°．请你帮助小红同学求出A、C两点之间的距离．（参考数据 ≈4.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

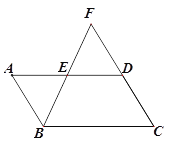
    【题目】如图，□ABCD中，E为AD的中点，BE、CD相交于点F.

    （1）求证：AB=DF

    （2）若△DEF的面积为S1，△BCF的面积为S2，且S12-S2+4=0，求□ABCD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

    (1)、求证：DE⊥AG；

    (2)、如图2，正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°），得到正方形OE′F′G′；

    ①在旋转过程中，当∠OAG′是直角时，求α的度数；

    ②若正方形ABCD的边长为2，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小红同学要测量A、C两地的距离，但A、C之间有一水池，不能直接测量，于是她在A、C同一水平面上选取了一点B，点B可直接到达A、C两地．她测量得到AB=80米，BC=20米，∠ABC=120°．请你帮助小红同学求出A、C两点之间的距离．（参考数据 ≈4.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】笔尖在纸上快速滑动写出了一个又一个字，这说明了；车轮旋转时，看起来像一个整体的圆面，这说明了；直角三角形绕它的直角边旋转一周形成了一圆锥体，这说明了.

    查看答案和解析>>

    同步练习册答案