
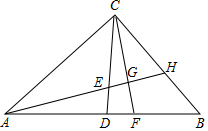
 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点 E、F移动过程中,点G移动路线的长度为( )| A. | 2 | B. | π | C. | 2 | D. | $\frac{{\sqrt{2}}}{2}$π |
分析 由△ADE≌△CDF,推出∠DAE=∠DCF,因为∠AED=∠CEG,推出∠ADE=∠CGE=90°,推出A、C、G、D四点共圆,推出点G的运动轨迹为弧CD,利用弧长公式计算即可.
解答 解:如图,
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,
∴∠ADE=∠CDF=90°,CD=AD=DB,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDF}\\{DE=DF}\end{array}\right.$,
∴△ADE≌△CDF(SAS),
∴∠DAE=∠DCF,
∵∠AED=∠CEG,
∴∠ADE=∠CGE=90°,
∴A、C、G、D四点共圆,
∴点G的运动轨迹为弧CD,
∵AB=4,AB=$\sqrt{2}$AC,
∴AC=2$\sqrt{2}$,
∴OA=OC=$\sqrt{2}$,
∵DA=DC,OA=OC,
∴DO⊥AC,
∴∠DOC=90°,
∴点G的运动轨迹的长为$\frac{90π×\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
故选D.
点评 本题考查等腰直角三角形的性质、轨迹、勾股定理、全等三角形的判定和性质,四点共圆等知识,解题的关键是正确探究点G的轨迹,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲体育生此次射击成绩的众数为7环 | |
| B. | 乙体育生此次射击成绩的平均数为7环 | |
| C. | 甲体育生此次射击成绩的成绩比乙体育生的稳定 | |
| D. | 乙体育生此次射击成绩的中位数为6环 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值为( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
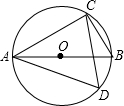 如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )
如图,已知AB是圆O的直径,∠CAB=30°,则cosD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
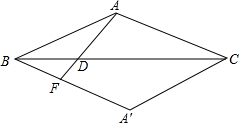 如图:等腰三角形ABC中,∠ABC=20°,将△ABC沿BC向下翻折得到△A′BC.已知D为线段BC上一点.连接AD,并延长AD交A′B于点F,若∠BAD=∠ABC,BF=3,CD=5,那么△ACD的面积为$\frac{15}{4}\sqrt{3}$.
如图:等腰三角形ABC中,∠ABC=20°,将△ABC沿BC向下翻折得到△A′BC.已知D为线段BC上一点.连接AD,并延长AD交A′B于点F,若∠BAD=∠ABC,BF=3,CD=5,那么△ACD的面积为$\frac{15}{4}\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com