
����Ŀ����ͼ����֪������y=��x2+bx+9��b2��bΪ��������������ԭ��O������x�ύ����һ��E���䶥��M�ڵ�һ���ޣ�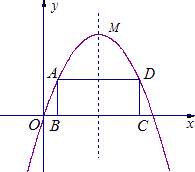
��1���������������Ӧ�ĺ�����ϵʽ��
��2�����A�Ǹ���������λ��x���Ϸ���������Գ�������һ�����㣻����A��x���ƽ���߽�������������һ��D������AB��x���ڵ�B��DC��x���ڵ�C��
�ٵ��߶�AB��BC�ij�������������λ����ʱ�������ABCD���ܳ���
�������ABCD���ܳ������ֵ����д����ʱ��A�����ꣻ
�۵�����ABCD���ܳ�ȡ�����ֵʱ����������Ƿ�Ҳͬʱȡ�����ֵ�����жϲ�˵�����ɣ�
���𰸡�
��1��
�⣺�����⣬����ԭ�㵽���κ�������ʽ
��9��b2=0��
���b=��3��
�����������ߵĶԳ������0��
![]() ��
��
����b=3��
���Խ���ʽΪy=��x2+3x
��2��
�⣺��A�������Ϊm���� ![]() ��m��0��
��m��0��
AB=3m��m2��BC=2�� ![]() ��m��=3��2m��
��m��=3��2m��
�����ABCD���ܳ�=2��AB+BC��=2����m2+m+3��=��2m2+2m+6��
�ٵ��߶�AB��BC�ij�������������λ����ʱ����
3m��m2��0��������3��2m��0��������
��m=1��
�����ABCD���ܳ�=��2m2+2m+6=6��
�ڡ߾���ABCD���ܳ�=��2m2+2m+6=��2��m2��m��+6=��2��m2��m+ ![]() ��
�� ![]() ��+6=��2��m��
��+6=��2��m�� ![]() ��2+
��2+ ![]() ��
��
�൱m= ![]() ʱ�������ֵ=
ʱ�������ֵ= ![]() ��
��
��m= ![]() ����y=��x2+3x��y=
����y=��x2+3x��y= ![]() ����A��������꣬
����A��������꣬
��ʱ��A������Ϊ�� ![]() ��
�� ![]() ����
����
�۵�����ABCD���ܳ�ȡ�����ֵʱ��m= ![]() ��
��
��ʱ����ABCD�����=ABBC=��3m��m2����3��2m��= ![]() ���������ֵ��
���������ֵ��
�ߵ�m= ![]() ʱ������ABCD�����=��3m��m2����3��2m��=1.6875��1.5=2.53125��
ʱ������ABCD�����=��3m��m2����3��2m��=1.6875��1.5=2.53125�� ![]() ��
��
�൱����ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ
����������1����֪�����߹�ԭ�㣬�������bֵ��������κ�������ʽ����2����A�������Ϊm���� ![]() ��m��0��AB=3m��m2 �� BC=3��2m������ABCD���ܳ�=��2m2+2m+6���ٸ����߶�AB��BC�ij�������������λ���ȼ�
��m��0��AB=3m��m2 �� BC=3��2m������ABCD���ܳ�=��2m2+2m+6���ٸ����߶�AB��BC�ij�������������λ���ȼ� ![]() ��m��0��ȷ��m��ֵ���Ӷ��������ABCD���ܳ����ڽ���2m2+2m+6�䷽�����ݶ��κ��������ʣ��ó�����ABCD���ܳ������ֵ���������ʱ��A�����ꣻ�۽�����ABCD���ܳ�ȡ�����ֵʱ��m��ֵ���������������ʽABBC=��3m��m2����3��2m���У��������ֵΪ2.5��Ȼ����
��m��0��ȷ��m��ֵ���Ӷ��������ABCD���ܳ����ڽ���2m2+2m+6�䷽�����ݶ��κ��������ʣ��ó�����ABCD���ܳ������ֵ���������ʱ��A�����ꣻ�۽�����ABCD���ܳ�ȡ�����ֵʱ��m��ֵ���������������ʽABBC=��3m��m2����3��2m���У��������ֵΪ2.5��Ȼ���� ![]() ��m��0�ķ�Χ���ҵ�һ��m=
��m��0�ķ�Χ���ҵ�һ��m= ![]() ʱ������ABCD�����=2.53125��
ʱ������ABCD�����=2.53125�� ![]() ���Ӷ��õ�������ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ��
���Ӷ��õ�������ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ��
�����㾫����������Ŀ����֪���������ö��κ�����ͼ������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�AB=4��AD=2����P�DZ�AB�ϵ�һ�����㣨�����A����B�غϣ�����Q�ڱ�AD�ϣ�����CBP�͡�QAP�ֱ���PC��PQ�۵���ʹB����E���غϣ�A����F���غϣ���P��E��F���㹲�ߣ�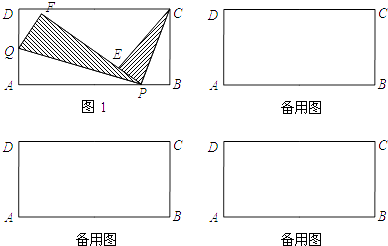
��1������Eƽ���߶�PF�����ʱAQ�ij�Ϊ���٣�
��2�����߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2�����ʱAP�ij�Ϊ���٣�
��3���ڡ��߶�CE�������߶�QF��������A���������У��Ƿ����������ͬһ��ֱ���ϵ�����������ڣ������ʱAP�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾Ϊ���˽�Ա��ÿ�������������������˾�Ӹ�����ȡ����Ա����ÿ�������������������ͳ�ƣ���������ͼ1��ͼ2ͳ��ͼ�� 
��1����ͼ����������
��2�����ι���ȡԱ���ˣ�ÿ������������������� �� ƽ��������
��3����ÿ�˴���������10��Ԫ������10��Ԫ������λ����Ա�����ڹ�˾1200Ա�����ж��ٿ�����Ϊ����Ա����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���졢�������ֱ�����180ǧ�ļס�������ͬʱ��������ͬһ·��������ʻ��������У��쳵�����ҵ�ͣ��һ��ʱ���ԭ·ԭ�ٷ��ؼأ���������رȿ쳵������� ![]() Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺
Сʱ�������ٶ��ǿ쳵�ٶȵ�һ�룬�졢����������غ�ֹͣ��ʻ����������Գ����ص�·��y��ǧ�ף�������ʱ��x��Сʱ���ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ����������⣺ 
��1����ֱ��д���졢���������ٶȣ�
��2����쳵���ع�����y��ǧ�ף���x��Сʱ���ĺ�����ϵʽ��
��3�������������ʱ�����90ǧ��·�̣�ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ı߳�Ϊ3cm������P�ӵ�A��������ÿ��1cm���ٶȣ���A��B��C�ķ����˶��������Cʱֹͣ�����˶�ʱ��Ϊx���룩��y=PC2 �� ��y����x�ĺ�����ͼ�����Ϊ�� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���˽�ѧ������������������������˲���ѧ��һ�ܲμ�����������ʱ�䣬�õ���ͼ������ͳ��ͼ������ͼ�ν���������⣺ 
��1����γ������ѧ����
��2��������ѧ��һ��ƽ���μ�������������Сʱ��
��3����֪��У��1200��ѧ�������Ƹ�У�ж�����ѧ��һ�ܲμ�����������ʱ�䳬��6Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ֪��y=�� ![]() x+3��x�ᡢy��ֱ���A��B���㣬��C(0��n)��y����һ�㣬������ƽ����ֱ��AC�۵���ʹ��B�պ�����x���ϣ����C��������( )
x+3��x�ᡢy��ֱ���A��B���㣬��C(0��n)��y����һ�㣬������ƽ����ֱ��AC�۵���ʹ��B�պ�����x���ϣ����C��������( )
A.(0�� ![]() )
)
B.(0�� ![]() )
)
C.(0��3)
D.(0,4)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y1=x��y2= ![]() ��ͼ����ͼ��ʾ�����й��ں���y=y1+y2�Ľ��ۣ��ٺ�����ͼ�����ԭ�����ĶԳƣ��ڵ�x��2ʱ��y��x���������С���۵�x��0ʱ��������ͼ����͵�������ǣ�2��4��������������ȷ���۵������ ��
��ͼ����ͼ��ʾ�����й��ں���y=y1+y2�Ľ��ۣ��ٺ�����ͼ�����ԭ�����ĶԳƣ��ڵ�x��2ʱ��y��x���������С���۵�x��0ʱ��������ͼ����͵�������ǣ�2��4��������������ȷ���۵������ �� 
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com