
【题目】如图,二次函数![]() 的图像与坐标轴分别交于
的图像与坐标轴分别交于![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() ,点
,点![]() 在
在![]() 轴正半轴上,连接
轴正半轴上,连接![]() 、
、![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 移动;同时点
移动;同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴向点
轴向点![]() 移动,它们移动的速度都是每秒1个单位长度,当其中一点到达终点时,另一点随之停止移动,连接
移动,它们移动的速度都是每秒1个单位长度,当其中一点到达终点时,另一点随之停止移动,连接![]() ,设移动时间为
,设移动时间为![]() .
.
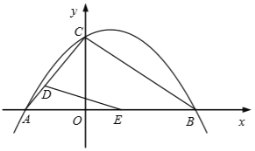
(1)若![]() 时,
时,![]() 与
与![]() 相似,求这个二次函数的表达式;
相似,求这个二次函数的表达式;
(2)若![]() 可以为直角三角形,求
可以为直角三角形,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)根据题意,可求得![]() 点坐标为(
点坐标为(![]() ,
,![]() ),当
),当![]() 时,可分别知道
时,可分别知道![]() ,
,![]() ,此时有两种情况,当
,此时有两种情况,当![]() 时,根据对应边成比例可以求得
时,根据对应边成比例可以求得![]() 的长度,即可知点
的长度,即可知点![]() 坐标,再利用待定系数法,即可求得此时的函数表达式;当
坐标,再利用待定系数法,即可求得此时的函数表达式;当![]() 时,根据比例关系求得
时,根据比例关系求得![]() ,不符合题意,故舍去;
,不符合题意,故舍去;
(2)若![]() 可以为直角三角形,可知
可以为直角三角形,可知![]() ,根据比例关系可求得
,根据比例关系可求得![]() 的长,设出点
的长,设出点![]() 的坐标(
的坐标(![]() ,
,![]() ),可知
),可知![]() ,所以抛物线的对称轴
,所以抛物线的对称轴![]() ,把点
,把点![]() 的坐标为(
的坐标为(![]() ,
,![]() )代入解析式,可知
)代入解析式,可知![]() 、
、![]() 之间的关系,消掉
之间的关系,消掉![]() ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
解:(1)把![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() (
(![]() ,
,![]() ),
),
∵![]() (
(![]() ,
,![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,点
,点![]() 坐标为(
坐标为(![]() ,
,![]() ).
).
把![]() ,
,![]() ;
;![]() ,
,![]() 分别代入
分别代入![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,
,
即![]() ,∴
,∴![]() (不符合题意,故舍去).
(不符合题意,故舍去).
综上,二次函数的表达式为![]() .
.
(2)若![]() 可以为直角三角形,显然
可以为直角三角形,显然![]() ,
,
∴![]() ,则
,则![]() ,设
,设![]() ,
,
即![]() ,解得:
,解得:![]() .
.
设![]() (
(![]() ,
,![]() ),则
),则![]() ,
,
设抛物线对称轴为直线![]() ,
,
∵![]() (
(![]() ,
,![]() ),∴
),∴![]() ①,
①,
把![]() ,
,![]() 代入
代入![]() ,得
,得![]() ②,
②,
把②代入①,且![]() ,
,
解得:![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
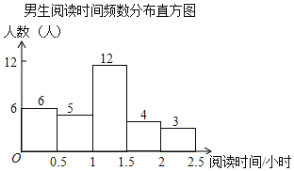
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边均和一条对角线相等的四边形叫做邻和四边形.
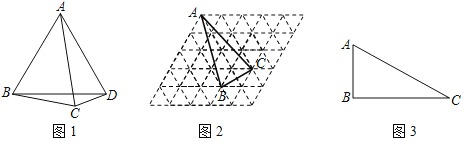
(1)如图1,四边形ABCD中,∠ABC=70°,∠BAC=40°,∠ACD=∠ADC=80°,求证:四边形ABCD是邻和四边形.
(2)如图2,是由50个小正三角形组成的网格,每个小正三角形的顶点称为格点,已知A,B,C三点的位置如图,请在网格图中标出所有的格点D,使得以A,B,C,D为顶点的四边形为邻和四边形.
(3)如图3,△ABC中,∠ABC=90°,AB=4,BC=4![]() ,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
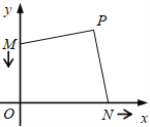
【题目】如图,动点![]() 从(0,3)出发,沿
从(0,3)出发,沿![]() 轴以每秒1个单位长度的速度向下移动,同时动点
轴以每秒1个单位长度的速度向下移动,同时动点![]() 从
从![]() 出发,沿
出发,沿![]() 轴以每秒2个单位长度的速度向右移动,当点
轴以每秒2个单位长度的速度向右移动,当点![]() 移动到
移动到![]() 点时,点
点时,点![]() 、
、![]() 同时停止移动.点
同时停止移动.点![]() 在第一象限内,在
在第一象限内,在![]() 、
、![]() 移动过程中,始终有
移动过程中,始终有![]() ,且
,且![]() .则在整个移动过程中,点
.则在整个移动过程中,点![]() 移动的路径长为( )
移动的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
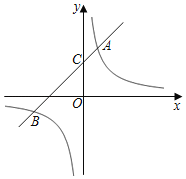
【题目】如图,在平面直角坐标系内xOy中,某一次函数的图象与反比例函数的y=![]() 的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
的图象交于A(1,m)、B(n,﹣1)两点,与y轴交于C点.
(1)求该一次函数的解析式;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com