
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����x2+bx+c��x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣬�����ߵĶԳ�����x����1������x�ύ��E�㣮
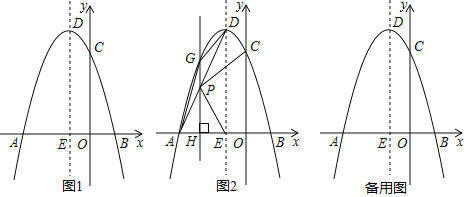
��1����ֱ��д�������ߵĽ���ʽ������D�����ꣻ
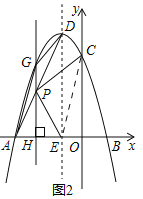
��2����ͼ2������AD�����P���߶�AD�ϵ�һ�����㣬����P��x��Ĵ��߽��������ڵ�G����x���ڵ�H������AG��GD������ADG�����Ϊ1ʱ��
�����P�����ꣻ
������PC��PE��̽��PC��PE��������ϵ��λ�ù�ϵ����˵������;
��3����MΪ��������һ���㣬NΪ�����ߵĶԳ�����һ���㣬QΪx����һ���㣬����Q��M��N��EΪ������ı���Ϊ������ʱ����ֱ��д����Q�����꣮
���𰸡���1��y����x2��2x+3������D����Ϊ����1��4������2����P����2��2������PC��PE��PC��PE�����ɼ���������3��Q��![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��
��������
��1�����ݴ���ϵ���������ɵõ��𰸣�
��2��������ֱ��AD�Ľ���ʽΪ��y��2x+6�����P��m��2m+6������3��m����1������G��m����m2��2m+3�����õ�PG=��m2��4m��3�����S��ADG��1���г�����m�ķ��̼��ɣ�
������CE�����ݹ��ɶ����ֱ����PC��PE�� CE��ֵ�����ɵõ�PC��PE��������ϵ��λ�ù�ϵ��
��3����N����1��n����Q��p��0������������ã�M��p��n����|p+1|��|n|����p2��2p+3��n�����������Q������.
��1����������y����x2+bx+c�ĶԳ�����x����1��
�ੁ![]() ����1��
����1��
��b����2��
��������y����x2+bx+c�Ľ���ʽΪy����x2��2x+c��
�������߹���A����3��0����
��0����9+6+c��
��c��3��
�������ߵĽ���ʽΪy����x2��2x+3��
�ඥ��D����Ϊ����1��4����
��2�����ɣ�1��֪��D����1��4����
��A����3��0����
��ֱ��AD�Ľ���ʽΪ��y��2x+6��
���P��m��2m+6������3��m����1����
�ɣ�1��֪�������ߵĽ���ʽΪ��y����x2��2x+3��
��PH��x�ᣬ
��G��m����m2��2m+3����
��PG����m2��2m+3����2m+6������m2��4m��3��
�ߡ�ADG�����Ϊ1��
��S��ADG��![]() PG������1+3������m2��4m��3��1��
PG������1+3������m2��4m��3��1��
��m����2��
��P����2��2����
����ͼ2������CE���ɣ�1��֪�������ߵĽ���ʽΪy����x2��2x+3��
��C��0��3����
�ɢ�֪��P����2��2����
�������ߵĶԳ���x��1��
��E����1��0����
��PC��![]() ��PE��
��PE��![]() ��
��![]() �� CE��
�� CE��![]() ��
��
��PC��PE��PC2+PE2��5+5��10��CE2��
���PCE����CEΪб�ߵ�ֱ�������Σ�
���CPE��90����
��PC��PE��
��3����N����1��n����Q��p��0����
����Q��M��N��EΪ������ı���Ϊ�����Σ�
��M��p��n����|p+1|��|n|�٣�
�ߵ�M���������ϣ�
�ੁp2��2p+3��n�ڣ�
�����٢ڽ�ã�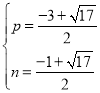 ��
�� ��
��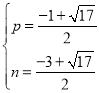 ��
�� ��
��
��Q��![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����![]() ��0����
��0����


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
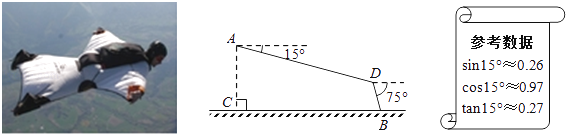
����Ŀ����ͼ��ij��װ����Ա����ˮƽ�����AC=500m��A�����������Ÿ���Ϊ15���ķ���ֱ����1600����D�㣬Ȼ�����ɡ��75���ĸ��ǽ��䵽�����ϵ�B�㣮�������е�ˮƽ����BC�������ȷ��1m����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳���4����E��AB����һ���㣬����CE������B��BG��CE�ڵ�G����P��AB������һ���㣬��PD+PG����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
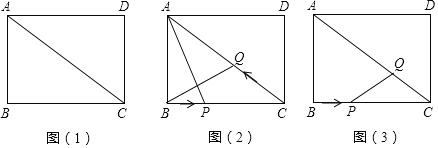
����Ŀ����ͼ,��֪�ı���ABCD��,AB//DC,AB=DC,��AB=6cm,BC=8cm,�Խ���AC =10cm,
(1)��֤:�ı���ABCD�Ǿ���;
(2)��ͼ(2),������Q�ӵ�C����,��CA������ÿ��5cm���ٶ����A�����˶�,ͬʱ����P�ӵ�B����,��BC������ÿ��4cm���ٶ����C�����˶�,�˶�ʱ��Ϊt��(0��t��2),����BQ��AP,��AP��BQ,��t��ֵ;
(3)��ͼ(3),����Q�ڶԽ���AC��,CQ=4cm,����P��B�����,��ÿ��1cm���ٶ���BC�˶�����Cֹ.���P�˶���t��,����̽��:���˶���ʼ,��������ʱ��,�Ե�Q��P��CΪ������������ǵ���������?��������п��ܵĽ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A1B1C1D1E1F1�ı߳�Ϊ1������6���Խ���Χ��һ����������A2B2C2D2E2F2����������A2B2C2D2E2F2��6���Խ�����Χ��һ����������A3B3C3D3E3F3������˼�����ȥ����������A4B4C4D4E4F4�������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У���D�ڱ�BC�ϣ�AE��BC��BE��AD��AC�ֱ��ཻ�ڵ�F��G�� ![]() ��
��
��1����֤����CAD�ס�CBG��
��2������DG����֤��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
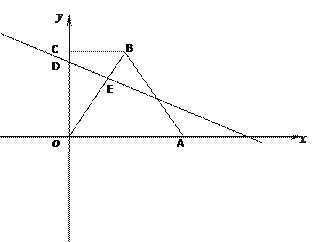
����Ŀ����ƽ��ֱ������ϵ�У�BC��OA��BC=3��OA=6��AB=3![]()
��1��ֱ��д����B������
��2����֪D.E�ֱ�Ϊ�߶�OC.OB�ϵĵ㣬OD=5��OE=2BE��ֱ��DE��x���ڵ�F����ֱ��DE�Ľ���ʽ
��3���ڣ�2���������£���M��ֱ��DE�ϵ�һ�㣬��x���Ϸ��Ƿ������һ����N��ʹ��O.D.M.NΪ������ı��������Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij����극����ʱ���Բ���һ���齱��Ϸ���������£���![]() ��ֽ�ƣ����ǵı��涼��С������ͷ������Ϊ
��ֽ�ƣ����ǵı��涼��С������ͷ������Ϊ![]() ��Ц����
��Ц����![]() �ſ������ֽ�
�ſ������ֽ�![]() ��ֽ��ϴ�Ⱥ��泯�ϰڷŵ����ϣ�Ȼ����������ȥ��ֽ�ƣ�
��ֽ��ϴ�Ⱥ��泯�ϰڷŵ����ϣ�Ȼ����������ȥ��ֽ�ƣ�
��1����С����һ�η��ƻ��ᣬ��������Ц���ľͻ������ǿ����IJ����������������һ��ֽ�ƣ�С��ĸ�����________��
��2������С�С�¶��з������ƵĻ��ᣬС���ȷ�һ�ţ��Żغ��ٷ�һ�ţ�С��ͬʱ��������ֽ�ƣ����Ƿ���������ֽ����ֻҪ����һ��Ц���ͻ�����˭�Ļ������Щ��ͨ������״ͼ���б�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
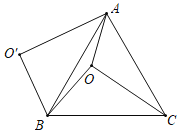
����Ŀ����ͼ��O������ABC��һ�㣬OA��6��OB��8��OC��10�����߶�BO�Ե�BΪ��ת������ʱ����ת60���õ��߶�BO'�����н��ۣ��١�BO'A��������BOC�Ƶ�B��ʱ����ת60���õ����ڵ�O��O���ľ���Ϊ6���ۡ�AOB��150������S��BOC��12+6![]() �� ��S�ı���AOBO����24+12
�� ��S�ı���AOBO����24+12![]() ��������ȷ�Ľ�����_____��������ţ�
��������ȷ�Ľ�����_____��������ţ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com