练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．崖城13-1气田是我国海上最大合作气田，年产气约为3400000000立方米，将数据3400000000用科学记数法表示为3.4×109．

    分析 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

    解答 解：3400000000=3.4×109，
    故答案为：3.4×109．

    点评 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    8．若点A（m，y1），B（m+1，y2）都在二次函数y=ax2+4ax+2（a＞0）的图象上，且y1＜y2，则m的取值范围是（　　）
    A．m＞-$\frac{5}{2}$B．m≥-2C．m＜-1D．m≤-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．小英同时掷甲、乙两枚质地均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．记甲立方体朝上一面上的数字为x，乙立方体朝上一面上分别标有数字为y，这样就确定点P的一个坐标（x，y），那么点P落在双曲线y=$\frac{6}{x}$上的概率为$\frac{1}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

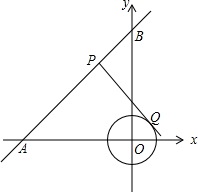    6．如图，在平面直角坐标系中，⊙O的半径为1，点P在经过点A（-3，0）、B（0，4）的直线上，PQ切⊙O于点Q，则切线长PQ的最小值为（　　）
    A．$\sqrt{7}$B．$\frac{\sqrt{119}}{5}$C．2.4D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

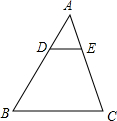    13．如图，在△ABC中，DE∥BC，$\frac{AD}{DB}$=$\frac{1}{2}$，则下列结论中正确的是（　　）
    A．$\frac{AE}{AC}$=$\frac{1}{2}$B．$\frac{DE}{BC}$=$\frac{1}{2}$
    C．$\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$D．$\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算：$\sqrt{2}×\sqrt{4}$=2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

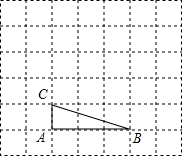    10．如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．
    （1）计算△ABC的面积等于$\frac{3}{2}$；
    （2）请在如图所示的网格中，用无刻度的直尺，画出一个以BC为一边的矩形，使该矩形的面积是△ABC面积的5倍，并简要说明画图方法（不要求证明）取格点D、E，连结CD、BE；再取格点M、N、P、Q，连结MN交CD于G，连结PQ交BE于H，连结GH，则四边形BCGH为所求．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

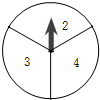    7．商场为了促销某件商品，设置了如图的一个转盘，它被分成了3个相同的扇形．各扇形分别标有数字2，3，4，指针的位置固定，该商品的价格由顾客自由转动此转盘两次来获取，每次转动后让其自由停止，记下指针所指的数字（指针指向两个扇形的交线时，当作右边的扇形），先记的数字作为价格的十位数字，后记的数字作为价格的个位数字，则顾客购买商品的价格不超过30元的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如果一条抛物线y=ax2+bx+c（a≠0）与x轴的两个交点为A，B（点A在点B的左侧），顶点为P，连接PA，PB，那么称△PAB为这条抛物线的“抛物线三角形”．
    （1）请写出“抛物线三角形”是等腰直角三角形时，抛物线的表达式（写出一个即可）y=-x2+1；
    （2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等边三角形，求b的值；
    （3）若△PAB是抛物线y=-x2+c的“抛物线三角形”，是否存在以点A为对称中心的矩形PBCD？若存在，求出过O，C，D三点的抛物线的表达式；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案