Question

13．如图，抛物线y=-x²+bx+c与x轴交于点M，N，与y轴交于点A（0，1），且经过点B（1，1），过点B作BC⊥x轴，交x轴于点C．
（1）求该抛物线的解析式．
（2）点E是线段OC上的一点（不与点O，C重合），AE⊥EF，且EF与∠BCN的平分线交于点F，当点E滑动到某处时，点F恰好落在抛物线上，求此时点E的坐标．
（3）在（2）的条件下y轴上是否存在点D，使得四边形BDEF是平行四边形？若存在，请求出点D的坐标，若不存在，请说明理由．

Answer 1

分析 （1）利用待定系数法求抛物线的解析式；
（2）如图1，作辅助线，构建全等三角形，设E（a，0），证明△AGE≌△ECF和△AOE≌△EHF，得出点F的坐标，再代入到抛物线的解析式中，求出a的值，根据已知进行取舍；
（3）由（2）中的a值，计算出点F的坐标，求出BF的长，即是ED的长，利用勾股定理可求得OD的长，写出点D的坐标．

解答 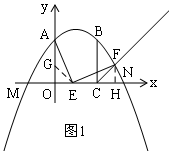解：（1）把点A（0，1），点B（1，1）分别代入抛物线y=-x²+bx+c得：
$\left\{\begin{array}{l}{c=1}\\{-1+b+c=1}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=1}\\{c=1}\end{array}\right.$，
∴该抛物线的解析式为：y=-x²+x+1；
（2）如图1，设E（a，0），则OE=a，
在AO上取一点G，使OG=OE，连接EG，
则△EOG是等腰直角三角形，
∴∠OGE=45°，
∴∠AGE=135°，
∵A（0，1），B（1，1），BC⊥OC，
∴OA=OC=1，
∴AG=EC，
∵FC平分∠BCN，∠BCN=90°，
∴∠FCN=45°，
∴∠ECF=135°，
∵AE⊥EF，
∴∠AEF=90°，
∴∠AEO+∠FEC=90°，
∵∠AOE=90°，
∴∠OAE+∠AEO=90°，
∴∠FEC=∠OAE，
∴△AGE≌△ECF，
∴AE=EF，
过F作FH⊥x轴于H，
∵∠AOE=∠EHF=90°，
∴△AOE≌△EHF，
∴EH=AO=1，FH=OE=a，
∴F（a+1，a），
∵F在抛物线上，
∴-（a+1）²+a+1+1=a，
解得：a₁=-1$+\sqrt{2}$，a₂=-1-$\sqrt{2}$，
∵点E是线段OC上的一点（不与点O，C重合），
∴0＜a＜1，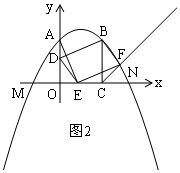
∴a=-1+$\sqrt{2}$，
∴E（-1+$\sqrt{2}$，0）；
（3）存在，如图2，
由（2）得：F（$\sqrt{2}$，$\sqrt{2}$-1），
由勾股定理得：BF=$\sqrt{（\sqrt{2}-1）^{2}+（1-\sqrt{2}+1）^{2}}$=$\sqrt{6}$-$\sqrt{3}$，
∵四边形BDEF是平行四边形，
∴ED=BF=$\sqrt{6}$-$\sqrt{3}$，
由勾股定理得：OD=$\sqrt{（\sqrt{6}-\sqrt{3}）^{2}-（\sqrt{2}-1）^{2}}$=2-$\sqrt{2}$，
∴D（0，2-$\sqrt{2}$）．

点评 本题是二次函数的综合题，考查了利用待定系数法求二次函数的解析式、全等三角形和等腰直角三角形的性质和判定、平行四边形的性质，本题是函数与几何图形的综合问题，利用全等三角形得出线段的长，根据点的坐标特征写出点的坐标．