
| A. | 两条对角线互相垂直平分的四边形是矩形 | |
| B. | 有一条对角线平分一组对角的四边形是菱形 | |
| C. | 两条对角线相等的四边形是矩形 | |
| D. | 一组对边平行,一组对角相等的四边形是平行四边形 |
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+c}{a+b}=\frac{c}{b}$ | B. | $\frac{a-c}{-a+b}=-\frac{a-c}{a+b}$ | ||
| C. | $\frac{x^8}{x^2}={x^4}$ | D. | $\frac{b}{{3{a^2}}}+\frac{1}{6ab}=\frac{{2{b^2}+a}}{{6{a^2}b}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | B. | 旅客上飞机前的安检 | ||
| C. | 了解全市中小学生每天的零花钱 | D. | 学校招聘教师,对应聘人员面试 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
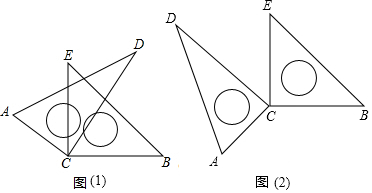
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com