
【题目】如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.
(1)求证:BE=CE;
(2)请直接写出∠ABC,∠ACB,∠ADE三者之间的数量关系;
(3)若∠ACB=40°,∠ADE=20°,求∠DCB的度数.
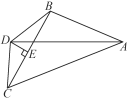
【答案】(1)见解析;(2)∠ABC-∠ACB=2∠ADE,理由见解析;(3)30°
【解析】
(1)利用等腰三角形底边上三线合一即可证明.
(2)结论:∠ABC-∠ACB=2∠ADE.如图2中,作BN⊥AD于N,交AC于M.证出∠ABN=∠AMN,再由角的和差求得。
(3)如图3中,作DM⊥AC于M,DN⊥AB于N.首先证明△DBN≌△DCM,推出∠BDN=∠CDM,推出∠CDB=∠MDN,由∠CAB+∠MDN=180°,推出∠CDB+∠CAB=180°,
利用(2)的结论求出∠ABC,∠CAB即可解决问题.
(1)证明:如图1中,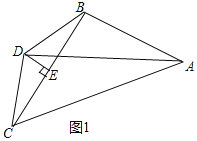
∵DB=DC,DE⊥BC,
∴CE=BE(等腰三角形底边上三线合一).
(2)结论:∠ABC-∠ACB=2∠ADE.
理由:如图2中,作BN⊥AD于N,交AC于M.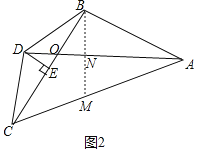
∵∠BAN=∠MAN,∠BAN+∠ABN=90°,∠MAN+∠AMN=90°,
∴∠ABN=∠AMN,
∵∠DOE=∠BON,∠DEO=∠BNO=90°,
∴∠EDA=∠CBM,
∴∠ABC-∠ACB=∠ABM+∠CBM-∠ACB=∠AMB+∠CBM-∠ABC=∠MCB+∠CBM+∠CBM-∠ACB=2∠CBN=2∠EDA.
故答案为∠ABC-∠ACB=2∠ADE
(3)解:如图3中,作DM⊥AC于M,DN⊥AB于N.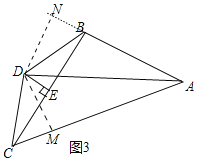
∵∠DAN=∠DAM,DM⊥AC,DN⊥AB,
∴DM=DN,
在Rt△DBN和Rt△DCM中,![]() ,
,
∴△DBN≌△DCM,
∴∠BDN=∠CDM,
∴∠CDB=∠MDN,
∵∠CAB+∠MDN=180°,
∴∠CDB+∠CAB=180°,
∵∠ACB=40°,∠ADE=20°,∠ABC-∠ACB=2∠ADE
∴∠ABC=80°,
∴∠CAB=180°-80°-40°=60°,
∴∠CDB=120°,
∴∠EDB=∠EDC=60°,
∴∠DCB=90°-∠EDC=30°.


科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A. ![]() B.
B. ![]() C. 5 D.
C. 5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
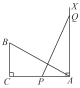
【题目】如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=_______________时,△ABC与△QPA全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的个数是( )
①2a2﹣a2=a2;
② ![]() +
+ ![]() =2
=2 ![]() ;
;
③(π﹣3.14)0× ![]() =0;
=0;
④a2÷a× ![]() =a2;
=a2;
⑤sin30°+cos60°= ![]() ;
;
⑥精确到万位6295382≈6.30×106 .
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点时停止,它们运动的速度都是每秒1个单位长度.设E运动x秒时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )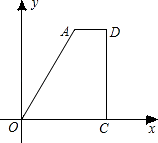
A.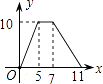
B.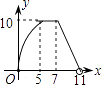
C.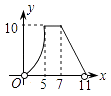
D.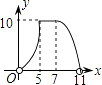
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
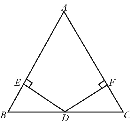
(1)求证;DE=DF;
(2)若∠A=90°,图中与DE相等的还有哪些线段?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )
A.b≥﹣1
B.b≤﹣1
C.b≥﹣2
D.b≤﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com