
【题目】如图,在矩形![]() 中,
中, ![]() =8
=8![]() ,
, ![]() =6
=6![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以2
以2 ![]() 的速度向终点
的速度向终点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() →
→![]() 以4
以4 ![]() 的速度向点
的速度向点![]() 匀速运动,到达点
匀速运动,到达点![]() 后,继续沿
后,继续沿![]() →
→![]() 以3
以3 ![]() 的速度向终点
的速度向终点![]() 匀速运动.连结
匀速运动.连结![]() ,以
,以![]() 、
、![]() 为边作□
为边作□![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (
(![]() ),□
),□![]() 与矩形
与矩形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() .
.
(1)当点![]() 在点
在点![]() 上,△
上,△![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
(2)当点![]() 在边
在边![]() 上,△
上,△![]() 与△
与△![]() 相似时,求
相似时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当△![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值.
的值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() (4)
(4)![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析:
(1) 由于△APQ为等腰直角三角形,所以AQ=AP. 根据对已知条件和动点的运动过程的分析,可以用x表示出线段AQ与AP的长. 根据AQ=AP可以得到一个关于x的方程,解这个方程即可得到满足条件的x值.
(2) 题干中给出的相似三角形有△CFQ∽△CAD与△CFQ∽△CDA两种情况. 需要据此分两种情况求解. 在第一种情况下,可以判定四边形APQD为平行四边形. 利用x表示出线段DQ与AP的长,可以得到一个关于x的方程,解这个方程即可得到满足条件的x值. 在第二种情况下,可以得到△CFQ与△AFP均为直角三角形. 在这两个直角三角形中,利用锐角三角函数可以得到线段CQ,AP以及AC的长度关系. 利用此关系列出方程求解即可.
(3) 分析题意可知,在PQ⊥AB之前,平行四边形BPQE与矩形ABCD重叠部分的面积为梯形BPQC的面积;在PQ⊥AB之后,平行四边形BPQE与矩形ABCD重叠部分的面积为平行四边形BPQE的面积,但是平行四边形BPQE面积的变化规律与点Q在线段CD还是AD上有关. 当点Q在线段CD上时,平行四边形BPQE的高不变;当点Q在线段AD上时,平行四边形BPQE的高随x的增大而减小. 根据上述分析,分三种情况讨论即可.
(4) 综合分析可知,△APF为等腰三角形有三种情况. 第一种情况下,AP=FP. 通过计算可以发现,当点Q在CD上时,线段AF的长是一个定值. 因此,通过等腰三角形“三线合一”的性质构造直角三角形,利用线段AF的长和锐角三角函数可以获得线段AP的长,进而获得x的值. 第二种情况下,AF=AP. 由线段AF的长容易得到线段AP的长,进而获得x的值. 第二种情况下,AF=PF. 在这种情况下,可以通过锐角三角函数的定义,利用线段AQ和AP的长度表达式,列出方程求解.
试题解析:
(1) 根据题意画出下列示意图.
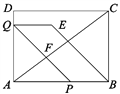
∵△APQ为等腰直角三角形,
又∵在矩形ABCD中,∠BAD=90°,
∴AP=AQ.
∵点P的运动时间为x (s),点P的运动速度为2 (cm/s),
∴AP=2x (cm).
∵当点Q在线段AD上时,点Q的运动路程为CD+DQ,
∵在线段CD上,点Q的运动速度为4 (cm/s),
又∵在矩形ABCD中,CD=AB=8cm,
∴点Q完成在线段CD上的运动需要2 (s).
∵点Q与点P同时开始运动,
∴点Q的运动时间为x (s),
∵在线段AD上,点Q的运动速度为3 (cm/s),
∴DQ=3(x-2) (cm),
∵在矩形ABCD中,AD=BC=6cm,
∴AQ=AD-DQ=6-3(x-2) (cm).
由AP=2x (cm),AQ =6-3(x-2) (cm),AP=AQ,可列关于x的方程:
2x=6-3(x-2),
解之,得
![]() (s).
(s).
∵点Q完成在线段CD上的运动需要2 (s),点P与点Q完成全部运动均需要4 (s),
∴在本小题中, ![]() ,
,
∴![]() 符合题意.
符合题意.
故当点Q在边AD上,△APQ是等腰直角三角形时,x的值为![]() .
.
(2) 分析题意可知,本小题应分以下两种情况分别求解.
①当△CFQ∽△CAD时,
∵△CFQ∽△CAD,
∴∠CFQ=∠CAD,
∴FQ∥AD,
∵在矩形ABCD中,AB∥CD,即AP∥DQ,
∴四边形APQD为平行四边形,
∴AP=QD.
∵在线段CD上,点Q的运动速度为4 (cm/s),点Q的运动时间为x (s),
∴CQ=4x (cm),
∴QD=CD-CQ=8-4x (cm),
由AP=2x (cm),QD=8-4x (cm),AP=QD,可列关于x的方程:
2x=8-4x,
解之,得
![]() (s).
(s).
∵点Q完成在线段CD上的运动需要2 (s),
∴在本小题中, ![]() ,
,
∴![]() 符合题意.
符合题意.
②当△CFQ∽△CDA时,
∵△CFQ∽△CDA,
∴∠CFQ=∠CDA,
∵在矩形ABCD中,∠CDA=90°,
∴∠CFQ=∠CDA=90°,
∴△CFQ与△AFP均为直角三角形.
∵AD=6cm,CD=8cm,
∴在Rt△CDA中, ![]() (cm),
(cm),
∴在Rt△CDA中, ![]() .
.
∵CQ=4x (cm),
∴在Rt△CFQ中, ![]() (cm).
(cm).
∵在矩形ABCD中,AB∥CD,
∴∠PAF=∠ACD,
∵AP=2x (cm),
∴在Rt△AFP中, ![]() (cm).
(cm).
由AF+CF=AC,可列关于x的方程:
![]() ,
,
解之,得
![]() (s).
(s).
∵在本小题中, ![]() ,
,
∴![]() 不符合题意.
不符合题意.
综上所述,当点Q在边CD上,△CFQ与△CAD相似时,x的值为![]() .
.
(3) ∵当PQ⊥AB时,AP=QD,
又∵AP=2x (cm),QD=8-4x (cm),
∴![]() (s).
(s).
又∵点Q完成在线段CD上的运动需要2 (s),
∴本小题应分别在![]() ,
, ![]() ,
, ![]() 三种情况下求解.(示意图如下)
三种情况下求解.(示意图如下)
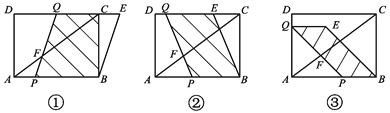
①当![]() 时,平行四边形BPQE与矩形ABCD重叠部分的面积y为梯形BPQC的面积.(如图①)
时,平行四边形BPQE与矩形ABCD重叠部分的面积y为梯形BPQC的面积.(如图①)
∵AB=8(cm),AP=2x(cm),
∴PB=8-2x(cm),
∵CQ=4x(cm),PB=8-2x(cm),BC=6(cm),
∴![]() .
.
②当![]() 时,平行四边形BPQE与矩形ABCD重叠部分的面积y为平行四边形BPQE的面积.(如图②)
时,平行四边形BPQE与矩形ABCD重叠部分的面积y为平行四边形BPQE的面积.(如图②)
∵QE=PB=8-2x(cm),BC=6(cm),
∴![]() .
.
③当![]() 时,平行四边形BPQE与矩形ABCD重叠部分的面积y为平行四边形BPQE的面积.(如图③)
时,平行四边形BPQE与矩形ABCD重叠部分的面积y为平行四边形BPQE的面积.(如图③)
∵DQ=3(x-2) (cm),
∴AQ=AD-DQ=6-3(x-2) (cm).
∵PB=8-2x(cm),AQ=6-3(x-2) (cm),
∴![]() .
.
综上所述,y与x之间的函数关系式为:
①当![]() 时,
时, ![]() ;
;
②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() .
.
(4) 当△APF为等腰三角形时,x的值为![]() ,
, ![]() ,
, ![]() . 求解过程如下.
. 求解过程如下.
综合分析可知,△APF为等腰三角形有如下图所示的三种情况.
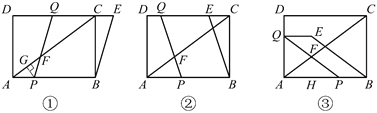
①若在图①所示的情形下,则AP=FP.
过点P作PG⊥AF,垂足为G.
∵在矩形ABCD中,AB∥CD,
∴当点Q在CD上时,△APF∽△CQF,
∵当点Q在CD上时,CQ=4x(cm),
又∵AP=2x (cm),
∴当点Q在CD上时, ![]() ,
,
∴当点Q在CD上时, ![]()
∵AC=10 (cm),
∴当点Q在CD上时, ![]() (cm).
(cm).
∵AP=FP,PG⊥AF, ![]() (cm),
(cm),
∴![]() (cm),
(cm),
∵![]() ,
,
∴在Rt△AGP中, ![]() (cm),
(cm),
∵AP=2x (cm),
∴![]() (s).
(s).
②若在图②所示的情形下,则AP=AF.
∵点Q在CD上,
∴![]() (cm),
(cm),
∵AP=2x (cm),
∴![]() (s).
(s).
③若在图③所示的情形下,则AF=PF.
∵AF=PF,
∴在△AFP中,∠FPA=∠PAF.
∵![]() ,
,
∴![]() .
.
∵AP=2x (cm),AQ=6-3(x-2) (cm),
∴在Rt△PAQ中, ![]() ,
,
∴![]() (s).
(s).
综上所述,当△APF为等腰三角形时,x的值为![]() ,
, ![]() ,
, ![]() .
.


科目:初中数学 来源: 题型:
【题目】两个完全相同的正四面体骰子的各面上分别标明数字1,2,3,4,在桌子上同时投掷这两个正四面体骰子,请用列表法或画树状图的方法,求与桌面接触的面所得的点数之和等于6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm![]() ?
?
(2)△PAQ的面积能否达到3 cm![]() ?
?
(3)经过多长时间,P、Q两点之间的距离为![]() cm?
cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过点M(4,-2)与点N(x,y)的直线平行于x轴,且点N到y轴的距离等于5,由点N的坐标是( )
A. (5,2)或(-5,-2)B. (5,-2)或(-5,-2)
C. (5,-2)或(-5,2)D. (5,-2)或(-2,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com