
分析 (1)根据|a+b-3|=-(ab-2)2,可以求得a、b的值,从而可以求得$\frac{b}{a}$+$\frac{a}{b}$的值;
(2)根据平方差公式和同底数幂的除法可以化简题目中的式子,然后将(1)中求得a、b的值代入即可解答本题.
解答 解:(1)∵|a+b-3|=-(ab-2)2,
∴|a+b-3|+(ab-2)2=0,
∴$\left\{\begin{array}{l}{a+b-3=0}\\{ab-2=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
∴当$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$时,$\frac{b}{a}$+$\frac{a}{b}$=$\frac{1}{2}+\frac{2}{1}$=$2\frac{1}{2}$,
当$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$时,$\frac{b}{a}$+$\frac{a}{b}$=$\frac{2}{1}+\frac{1}{2}$=$2\frac{1}{2}$;
(2)(a-b+1)(b-a+1)+2a3b÷(-$\frac{1}{2}$a)2
=[1+(a-b)][1-(a-b)]+$2{a}^{3}b÷\frac{1}{4}{a}^{2}$
=1-(a-b)2+8ab
=1-a2+2ab-b2+8ab
=1-a2+10ab-b2,
当$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$时,原式=1-22+10×2×1-12=16,
当$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$时,原式=1-12+10×1×2-22=16.
点评 本题考查分式的化简求值、非负数的性质、整式的化简求值,解答本题的关键是明确它们各自的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
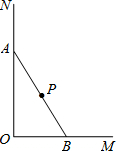 如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )
如图,木杆AB斜靠在墙壁上,∠OAB=30°,AB=4米.当木杆的上端A沿墙壁NO下滑时,木杆的底端B也随之沿着地面上的射线OM方向滑动.设木杆的顶端A匀速下滑到点O停止,则木杆的中点P到射线OM的距离y(米)与下滑的时间x(秒)之间的函数图象大致是( )| A. | 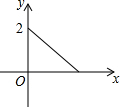 | B. | 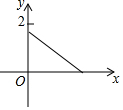 | C. | 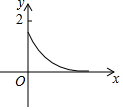 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 “奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.
“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是20$\sqrt{6}$m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
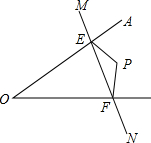 如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.
如图所示,点P在∠AOB内部,点M、N分别是点P关于AO、BO的对称点,若△PEF的周长为13cm,ME=3cm,FN=4cm,则EF=6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com