
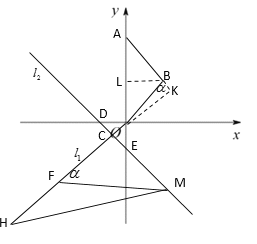
【题目】已知抛物线![]() 经过点
经过点![]() ,点
,点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的顶点
的顶点![]() ,且
,且![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,若把抛物线上下平移,使抛物线的顶点在直线
,若把抛物线上下平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ),再把抛物线左右平移,使抛物线的顶点在直线
),再把抛物线左右平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ).
).
(1)求抛物线![]() 的解析式.
的解析式.
(2)判断以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设点![]() 、
、![]() 在直线
在直线![]() 上(点
上(点![]() 在点
在点![]() 的下方),当
的下方),当![]() 与
与![]() 相似时,求
相似时,求![]() 、
、![]() 的坐标(直接写出结果).
的坐标(直接写出结果).

【答案】(1)![]() ;(2)相离,理由详见解析;(3)
;(2)相离,理由详见解析;(3)![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]()
【解析】
(1)将点A、B的坐标代入![]() 即可求出解析式;
即可求出解析式;
(2)求出点N、C的坐标,计算NC的长度即可求解;
(3)分点F在直线![]() 下方,上方两种情况求解.
下方,上方两种情况求解.
(1)将点A、B的坐标代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)∵![]() ,
,
∴顶点坐标是(2,2),
将点P的坐标代入直线![]() 中,得2k=2,即k=1,
中,得2k=2,即k=1,
∴直线![]() 的解析式是y=x,
的解析式是y=x,
设点M(2,m),代入直线![]() 的解析式中,得m=-4,
的解析式中,得m=-4,
∴点M的坐标是(2,-4),
设点N的坐标是(n,-4),代入![]() 的解析式中,得n=-4,
的解析式中,得n=-4,
∴点N的坐标是(-4,-4),
同理:D(-2,0),E(0,-2),
联立![]() 、
、![]() 得
得![]() ,得
,得![]() ,
,
∴C(-1,-1),
∴OC=![]() ,
,
∴![]() ,
,
∵点C在直线y=x上,
∴∠COE=∠OEC=45°,
∴∠OCE=90°,即NC⊥![]() ,
,
∵NC=![]()
∴以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 相离;
相离;
(3)①当点F在直线![]() 下方时,
下方时,
设![]() ,
,
∵点A、B的坐标分别为(0,6),(1,3),
∴AO=6,AB=BO=![]() ,
,
过点B作BL⊥y轴于L,则![]() ,
,![]() ,
,
∴OK=![]() ,
,
∴![]() ,
,
∵等腰△MHF和等腰△OAB相似,
∴∠HFM=∠ABO,则∠KBO=∠OFM=![]() ,
,
∵C(-1,-1),M(2,-4),
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴F(-5,-5),
∵FH=FM=![]() ,OH=OF+FH=
,OH=OF+FH=![]() ,
,
∴H(-10,-10);
②当点F在直线![]() 上方时,
上方时,
同理可得点F的坐标为(8,8),点H的坐标为(3,3)或(-10,-10);
综上,![]() 、
、![]() 或
或![]() 、
、![]() 或
或![]() 、
、![]()


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接 AC、OD交于点E.
(1)若tan∠ABC=2,证明:DA与⊙O相切:
(2)在(1)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
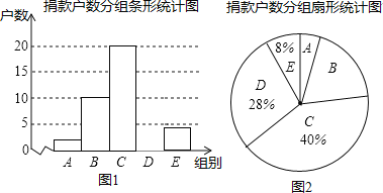
【题目】某社区组织“献爱心”捐款活动,并对部分捐款户数进行调查和分组统计,数据整理成如下统计图表(图中信息不完整).
捐款户数分组统计表
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<100 | 2 |
B | 100≤x<200 | 10 |
C | 200≤x<300 | c |
D | 300≤x<400 | d |
E | x≥400 | e |
请结合以上信息解答下列问题:
(1)本次调查的样本容量是______;
(2)d=______,并补全图1;
(3)图2中,“B”所对应扇形的圆心角为______度;
(4)若该社区有500户住户,根据以上信息估计全社区捐款不少于300元的户数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
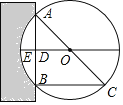
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上). 现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分钟)之间的关系如图2所示.①图2中折线ABC表示___________槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2﹣4ax+2a(a≠0)
(1)求抛物线的对称轴;
(2)若抛物线经过点A(m,y1),B(n,y2),其中﹣4<m≤﹣3,2<n≤3,请依据a的取值情况直接写出y1与y2的大小关系;
(3)若矩形CDEF的顶点分别为C(1,2),D(1,﹣4),E(5,﹣4),F(5,2),若该抛物线与矩形的边有且只有两个公共点(包括矩形的顶点),求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店在“读书节”之前,图书按标价销售,在“读书节”期间制定了活动计划.
(1)“读书节”之前小明发现:购买5本A图书和8本B图书共花279元,购买10本A图书比购买6本B图书多花162元,请求出A、B图书的标价;
(2)“读书节”期间书店计划用不超过3680元购进A、B图书共200本,且A图书不少于50本,A、B两种图书进价分别为24元、16元;销售时准备A图书每本降价1.5元,B图书价格不变,那么书店如何进货才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、点
、点![]() 分别在线段
分别在线段![]() 、线段
、线段![]() 上运动(不包含端点),以
上运动(不包含端点),以![]() 为边作平行四边形
为边作平行四边形![]() ,点
,点![]() 从
从![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位长度,点
个单位长度,点![]() 从
从![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位长度,两点同时出发,当一个点到达终点时,两点都停止运动,运动时间为
个单位长度,两点同时出发,当一个点到达终点时,两点都停止运动,运动时间为![]() 秒.
秒.
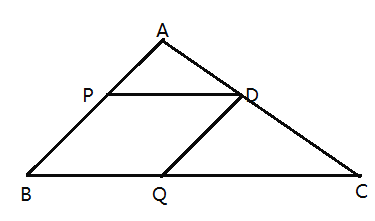
(1)![]() __ ,
__ ,![]() __ _; (用
__ _; (用![]() 表示)
表示)
(2)当平行四边形![]() 为菱形时,求出
为菱形时,求出![]() 值;
值;
(3)![]() 点能否落在线段
点能否落在线段![]() 上?若能,求出
上?若能,求出![]()
(4)当![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点时,求
两点时,求![]() 长度的范围;
长度的范围;
(5)平行四边形![]() 的面积能否为
的面积能否为![]() 面积的一半,若能,请求出
面积的一半,若能,请求出![]() 值,若不能,请说明理由.
值,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com