
 如图,在?ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC于点F,DF=2.求EF的长.
如图,在?ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC于点F,DF=2.求EF的长.
| ||
| 2 |
| 3 |


科目:初中数学 来源: 题型:
 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交 |
| AB |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.
如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.查看答案和解析>>
科目:初中数学 来源: 题型:
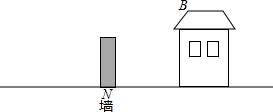 如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来.
如图,小区管理者打算在广场的地面上安装一盏路灯(路灯高度忽略不计).小明此刻正在某建筑物的B处向下看,请问:此路灯安在什么位置,小明在B处看不到?请把这段范围用线段表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com