
【题目】如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
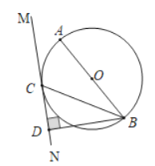
(1)求证:∠ABC=∠CBD;(2)若BC=4![]() ,CD=4,则⊙O的半径是 .
,CD=4,则⊙O的半径是 .
【答案】(1)见解析;(2)5.
【解析】
(1)连接OC,由切线的性质可得OC⊥MN,即可证得OC∥BD,由平行线的性质和等腰三角形的性质可得∠CBD=∠BCO=∠ABC,即可证得结论;
(2)连接AC,由勾股定理求得BD,然后通过证得△ABC∽△CBD,求得直径AB,从而求得半径.
(1)证明:连接OC,
∵MN为⊙O的切线,
∴OC⊥MN,
∵BD⊥MN,
∴OC∥BD,
∴∠CBD=∠BCO.
又∵OC=OB,
∴∠BCO=∠ABC,
∴∠CBD=∠ABC.;
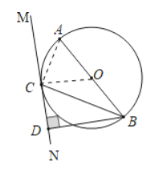
(2)解:连接AC,
在Rt△BCD中,BC=4![]() ,CD=4,
,CD=4,
∴BD=![]() =8,
=8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠CDB=90°,
∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴![]() ,即
,即![]() ,
,
∴AB=10,
∴⊙O的半径是5,
故答案为5.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A(2,1),B两点.
的图象相交于A(2,1),B两点.
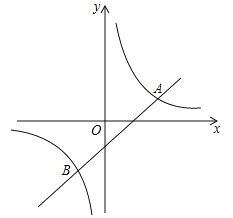
(1)求出反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
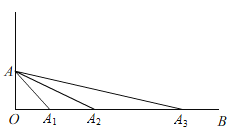
【题目】如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依此作法,则∠AA2A3=___,∠AAnAn+1等于___度.(用含n的代数式表示,n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
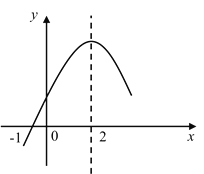
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③ 8a+7b+2c>0;④若点A(﹣3,y1)、点B(![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;⑤若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有_______个.
,y3)在该函数图象上,则y1<y3<y2;⑤若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
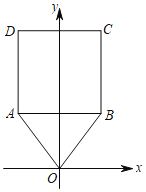
【题目】如图,平面直角坐标系中,已知O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,测第70次旋转结束时,点D的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发:
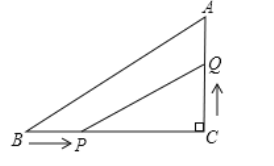
(1)经过多少秒后,△CPQ的面积为8cm?
(2)经过多少秒时,以C、P、Q为顶点的三角形恰与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
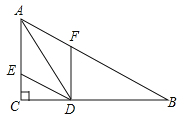
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年元且,某商场为促销举办抽奖活动.规则如下:在一个不透明的纸盒里,装有2个红球和2个黑球,这些球除颜色外都相同.顾客每次摸出1个球,若摸到红球,则获得一份奖品;若摸到黑球,则没有奖品.
(1)如果张大妈只有一次摸球机会,那么张大妈获得奖品的概率是 .
(2)如果张大妈有两次摸球机会(摸出后不放回),请用“树状图”或“列表”的方法,求张大妈获得两份奖品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 号楼在
号楼在![]() 号楼的南侧,两楼高度均为
号楼的南侧,两楼高度均为![]() 楼间距为
楼间距为![]() .冬至日正午,太阳光线与水平面所成的角为
.冬至日正午,太阳光线与水平面所成的角为![]() .
.![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() ,春分日正午,太阳光线与水平面所成的角为
,春分日正午,太阳光线与水平面所成的角为![]() ,
,![]() 号楼在
号楼在![]() 号楼墙面上的影高为
号楼墙面上的影高为![]() .已知
.已知![]() .
.
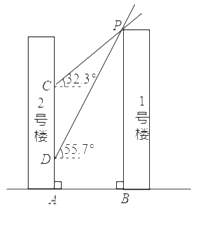
(1)求楼间距![]() ;
;
(2)若![]() 号楼共
号楼共![]() 层,层高均为
层,层高均为![]() 则点
则点![]() 位于第几层? ( 参考数据:
位于第几层? ( 参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com