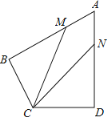
【题目】如图，在四边形ABCD中，AB=AD=6，AB⊥BC，AD⊥CD，∠BAD=60°，点M、N分别在AB、AD边上，若AM：MB=AN：ND=1：2．则∠BCD= °，cos∠MCN= ．
【答案】120 ；
【解析】
试题分析：∵在四边形ABCD中， AB⊥BC，AD⊥CD，∠BAD=60°， ∴∠BCD=360°-90°-90°-60°=120°；
连接MN，连接AC，
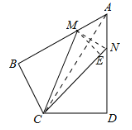
∵AB=AD=6，AM：MB=AN：ND=1：2，∴AM=AN=2，BM=DN=4，∵∠MAN=60°，∴△MAN是等边三角形，∴MN=AM=AN=2，
∵在Rt△ABC与Rt△ADC中，
，∴Rt△ABC≌Rt△ADC（HL），∴∠BAC=∠DAC=
∠BAD=30°，MC=NC，∴BC=AC，∴AC2=BC2+AB2，即（2BC）2=BC2+AB2，3BC2=AB2，∴BC=
，
在Rt△BMC中，CM=
=
，
过M点作ME⊥ON于E，设NE=x，则CE=
-x，
∴MN2-NE2=MC2-EC2，即4-x2=（）2-（-x）2，
解得：x=
，∴EC=-=
，∴cos∠MCN=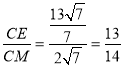
．
科目：初中数学 来源： 题型：
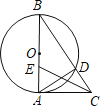
【题目】如图，在△ABC中，以AB为直径的⊙O交BC于点D，∠DAC＝∠B．
（1）求证：CA是⊙O的切线．
（2）在AB上取一点E，若∠BCE＝∠B，AB＝2AC，求tan∠ACE的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某果农在其承包的果园中种植了60棵桔子树，每棵桔子树的产量是100kg，果农想增加桔子树的棵数来增产，但增加果树会导致每棵树的光照减少，使得单棵果树产量减少，试验发现每增加1棵桔子树，单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下，增加多少棵桔子树时，可以使果园总产量达到6650kg？
(2)设增加x棵桔子树，考虑实际增加桔子树的情况，10≤x≤40，请你计算一下，果园总产量最多为多少kg，最少为多少kg？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y1：y＝2（x﹣3）2+1和抛物线y2：y＝﹣2x2﹣8x﹣3，若无论k取何值，直线y＝kx+km+n被两条抛物线所截的两条线段都保持相等，则m＝_____，n＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
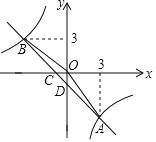
【题目】如图，一次函数y＝kx+b(k，b为常数，k≠0)的图象与反比例函数
的图象交于A、B两点，且与x轴交于点C，与y轴交于点D，A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式；
(2)求△AOB的面积；
(3)写出不等式kx+b＞﹣
的解集.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某大学生创业团队有研发、管理和操作三个小组，各组的日工资和人数如下表所示．现从管理组分别抽调1人到研发组和操作组，调整后与调整前相比，下列说法中不正确的是（ ）
操作组 | 管理组 | 研发组 | |
日工资（元/人） | 260 | 280 | 300 |
人数（人） | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点H，点F是
上一点，连接AF交CD的延长线于点E．
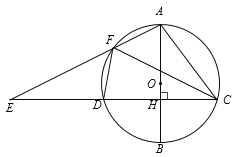
（1）求证：△AFC∽△ACE；
（2）若AC＝5，DC＝6，当点F为的中点时，求AF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
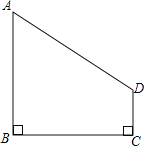
【题目】在四边形ABCD中，∠B＝∠C＝90°，若AB＝4，BC＝4，CD＝1，问：在BC上是否存在点P，使得AP⊥PD？若存在，求出BP的长；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，以
为直径作
，点D在上，
，
，垂足为点E，
与和
分别交于点M、F．连接
、
、
．
（1）证明：
是的切线；
（2）若
，
，求的半径长；
（3）在（2）的条件下，求
的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com