
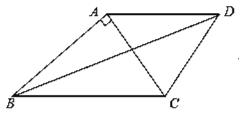
【题目】如图,AD∥BC,AC⊥AB,AB=3,AC=CD=2.
(1)求BC的长;
(2)求BD的长.
【答案】(1)BC=![]() ;(2)BD=5
;(2)BD=5
【解析】
(1)在Rt△ABC中利用勾股定理即可求出BC的长;
(2)过点B作BE⊥DC交DC的延长线于点E.根据等边对等角的性质以及平行线的性质得出∠2=∠3,利用角平分线的性质得出AB=BE=3,在Rt△BCE中,根据勾股定理可得EC=2,则ED=4,在Rt△BDE中,利用勾股定理可得BD=5.
(1)在Rt△ABC中,∵AC⊥AB,AB=3,AC=2,
∴BC=![]() ;
;
(2)过点B作BE⊥DC交DC的延长线于点E.
∵AC=CD,
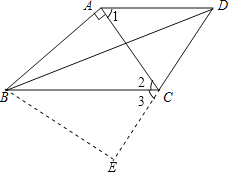
∴∠1=∠ADC,
又∵AD∥BC,
∴∠3=∠ADC,∠1=∠2,
∴∠2=∠3,
又∵AC⊥AB,BE⊥DC,
∴AB=BE=3,
又由(1)BC=![]() ,
,
在Rt△BCE中,由勾股定理可得EC=2;
∴ED=2+2=4,
在Rt△BDE中,由勾股定理可得BD=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
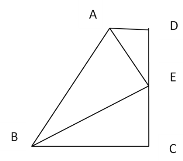
【题目】如图, 在四边形ABCD中,AD∥BC, E为CD的中点,连接 AE 、BE ,BE⊥AE, 延长AE交BC的延长线于 F,求证:(1) BE平分∠ABC (2)AB=BC+AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古巴比伦的记数法是六十进制的,用 ![]() 表示1,用
表示1,用 ![]() 表示10,这两种符号能表示一直到59的数字,例如,32可以用
表示10,这两种符号能表示一直到59的数字,例如,32可以用 ![]() 表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如,
表示。从60起,开始使用符号组,从右往左依次是个位、六十位、三千六百位……(每一位的数值都是上一位的60倍),例如, ![]() 的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( )
的个位表示23个1,六十位表示2个60,所以这个符号表示143。则下列表示3812的符号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C,D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨:从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨,现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求y与x的函数关系式.
(3)怎样调运才能使总运费最少?并求最少运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
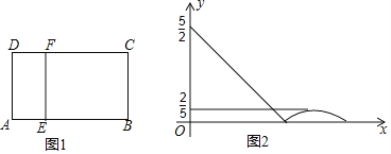
【题目】如图1,在矩形ABCD中,动点E从A出发,沿![]() 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做![]() ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, ![]() ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B.
B. ![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.
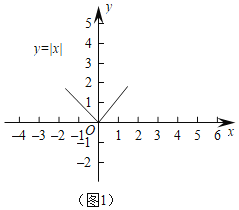
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com