


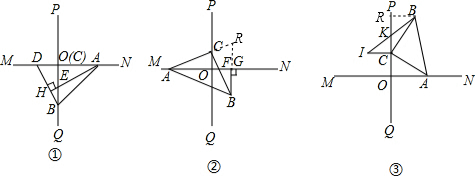
 (1)证明:如图①,
(1)证明:如图①,
|
|
|
| BR |
| IC |
| RK |
| KC |
| 1 |
| 2 |
| 1 |
| 2 |


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
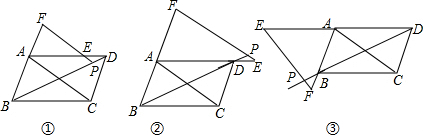
 如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF
如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF查看答案和解析>>
科目:初中数学 来源: 题型:
 已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?
已知△ABC,AB=AC=5cm,BC=8cm,P为AC上一动点,沿着折线CAB运动(当到达B时停止),Q为CB上一动点,沿CB运动(到B时停止),若P,Q分别同时从C点出发,以2cm/s和1cm/s的速度沿折线CAB和CB运动,问,何时PQ截△ABC两边所形成的三角形与原三角形相似?是位似图形吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.
有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数y=
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数y=| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com