
 的解,所以这个方程组的解是
的解,所以这个方程组的解是 在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它的右下方的部分,如图③.
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它的右下方的部分,如图③. 的解;
的解; 所围成的平面区域,并求围成区域的面积;
所围成的平面区域,并求围成区域的面积; 右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?
右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?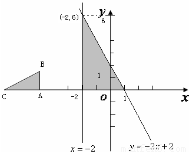 解:(1)如图,由图象可得方程组的解是
解:(1)如图,由图象可得方程组的解是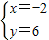 ;
;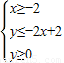 所围成的平面区域如图所示;
所围成的平面区域如图所示;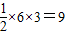 ;
;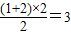 ;
;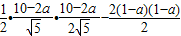 -
- =
=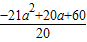 ,
,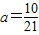 时
时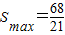 ;
;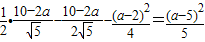 -
-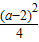 =
=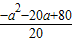 ,
,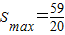 ;
; ;
;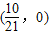 时,小车被挡住的面积最大为
时,小车被挡住的面积最大为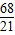 .(12分)
.(12分)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:阅读理解
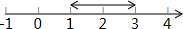




| 2 |
| 3 |
| 1 |
| 4 |
| 8 |
| 9 |
| 1 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 28、
28、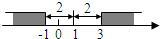 阅读下列材料:
阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
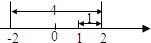
 x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:
x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com