
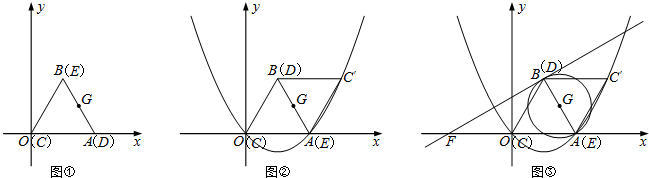
���� ��1�����õȱ������ε����ʣ����������
��2�����ô���ϵ������������κ�������ʽ�����������
��3���������ߵ����ʶ�����ֱ�������ε����ʣ����F��B�����꼴���������ʽ��
��4�������P����ó���Q���꣬�Ӷ��ó�PQ=-$\frac{\sqrt{3}}{3}$��m-$\frac{3}{2}$��2+$\frac{17\sqrt{3}}{12}$��
��� ��1����ͼ�ڣ�
����B��BH��OA��
�ߵȱ�������OAB�ı߳�Ϊ2��
��BH=$\sqrt{3}$��OH=1��
����ת�ã�BC=OA=2��
��C'��3��$\sqrt{3}$����
��2���������߹�ԭ��O��0��0�����������߽���ʽΪy=ax2+bx��
��A��2��0����C�䣨3��$\sqrt{3}$�����룬�ã�$\left\{\begin{array}{l}{4a+2b=0}\\{9a+3b=\sqrt{3}}\end{array}\right.$��
���a=$\frac{\sqrt{3}}{3}$��b=-$\frac{2\sqrt{3}}{3}$��
�������߽���ʽΪy=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x��
��3���ߡ�ABF=90�㣬��BAF=60�㣬
���AFB=30�㣬
�֡�AB=2��
��AF=4��
��OF=2��
��F��-2��0����
��ֱ��BF�Ľ���ʽΪy=kx+b'��
��B��1��$\sqrt{3}$����F��-2��0�����룬�ã�$\left\{\begin{array}{l}{k+b'=\sqrt{3}}\\{-2k+b'=0}\end{array}\right.$��
���k=$\frac{\sqrt{3}}{3}$��b'=$\frac{2\sqrt{3}}{3}$��
��ֱ��BF�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$��
��4����ͼ�ۣ�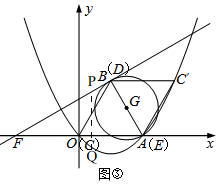
����P��PQ��x�ᣬ����������Q��
�ɣ�3��֪��ֱ��BF�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$�٣�
��P��m��$\frac{\sqrt{3}}{3}$m+$\frac{2\sqrt{3}}{3}$����
��Q��m��$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m����
��PQ=$\frac{\sqrt{3}}{3}$m+$\frac{2\sqrt{3}}{3}$-��$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m��=-$\frac{\sqrt{3}}{3}$��m-$\frac{3}{2}$��2+$\frac{17\sqrt{3}}{12}$��
�൱m=$\frac{3}{2}$ʱ��PQ���=$\frac{17\sqrt{3}}{12}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˵ȱ������ε����ʣ���ת�����ʣ�����ϵ���������ߵ����ʣ�ֱ�������ε����ʣ��Ȿ��Ĺؼ������ֱ�������Σ���һ���ۺ��ԱȽ�ǿ���п������⣮


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
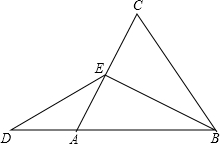 ��ͼ���ڵȱ�������ABC�У�BE��AC�ϵ����ߣ�D��BA���ӳ����ϣ�AE=AD����˵����DE=EB��
��ͼ���ڵȱ�������ABC�У�BE��AC�ϵ����ߣ�D��BA���ӳ����ϣ�AE=AD����˵����DE=EB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ӣ����ڲ������� | B�� | ����ȷ��Բ | ||
| C�� | ʵ��a��0����2a��0 | D�� | �½��Ķ��첻��ѩ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
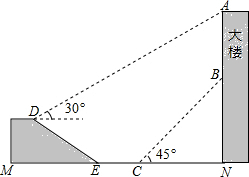
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���������� | B�� | ������ | C�� | ֱ�������� | D�� | ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com