
【题目】如图,矩形ABCD中,AB=4,AD=3,∠DAB的角平分线交边CD于点E.点P在射线AE上以每秒![]() 个单位长度的速度沿射线AE方向从点A开始运动;过点P作PQ⊥AB于点Q,以PQ为边向右作平行四边形
个单位长度的速度沿射线AE方向从点A开始运动;过点P作PQ⊥AB于点Q,以PQ为边向右作平行四边形![]() ,点N在射线AE上,且AP=PN.设P点运动时间为t秒.
,点N在射线AE上,且AP=PN.设P点运动时间为t秒.
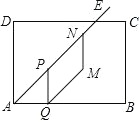
(1)PQ= (用含t的代数式表示).
(2)当点M落在BC边上时,求t的值.
(3)设平行四边形PQMN与矩形ABCD重合部分面积为S,当点P在线段AE上运动时,求S与t 的函数关系式.
(4)直接写出在点P、Q运动的过程中,整个图形中形成的三角形存在全等三角形时t的值(不添加任何辅助线).
【答案】(1)t;(2)2;(3)当0≤t≤![]() 时,
时,![]() ;当
;当![]() ≤2时,
≤2时,![]() ;当
;当![]() ≤3时,
≤3时,![]() ;(4)2或3或
;(4)2或3或![]()
【解析】
(1)判断出ΔAPQ是等腰三角形即可得出结结论;
(2)由AP=PN判断出Q为AB的中点,进而求得AQ=2,即可得出结论;
(3)分三种情况讨论:①当0﹤t≤![]() 时,重合部分是平行四边形PQMN;②当
时,重合部分是平行四边形PQMN;②当![]() ≤2时,重合部分是五边形PQMGE,③当
≤2时,重合部分是五边形PQMGE,③当![]() ≤3时,重合部分是五边形PQGCE,分别求解即可;
≤3时,重合部分是五边形PQGCE,分别求解即可;
(4)也是分三种情况讨论:①当点Q是AB的中点时,ΔAPQ≌ΔQMB;②当点P与点E重合时,ΔAPQ≌ΔEAD;③当ΔPEK≌ΔQGB时,分别求解即可.
(1)∵四边形ABCD是矩形,
∴∠BAD=90,
∵AE平分∠BAD,
∴∠BAE=45,
∵PQ⊥AB,
∴ΔAPQ是等腰直角三角形,
由运动知,AP=![]() t,
t,
∴PQ= t;
(2)如图2,当点M落在BC上时,
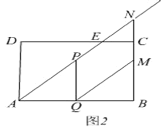
∵四边形PQMN是平行四边形,
∴PQ∥MN,即PQ∥BN,
∵AP=PN,
∴AQ=QB=2.
∵∠NAB =45°,
∴PQ=AQ=2.
∴t=2
(3)①当0≤t≤![]() 时,如图4,重合部分是平行四边形PQMN,
时,如图4,重合部分是平行四边形PQMN,![]() ;
;

②当![]() ≤2时,如图5,重合部分是五边形PQMGE,
≤2时,如图5,重合部分是五边形PQMGE,
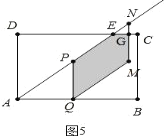
![]() ;
;
③当![]() ≤3时,如图6,重合部分是五边形PQGCE,
≤3时,如图6,重合部分是五边形PQGCE,
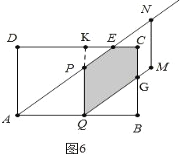
![]() =
=![]() ,
,
综上,当0≤t≤![]() 时,
时,![]() ;当
;当![]() ≤2时,
≤2时,![]() ;当
;当![]() ≤3时,
≤3时,![]() ;.
;.
(4)①如图7,当点Q是AB的中点时,ΔAPQ≌ΔQMB,此时![]() ;
;
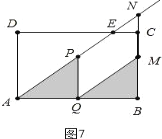
②如图8,当点P与点E重合时,ΔAPQ≌ΔEAD,![]() ,
,
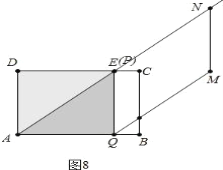
③如图9,当ΔPEK≌ΔQGB时,由EK=BQ得:t-3=4-t,解得![]() .
.
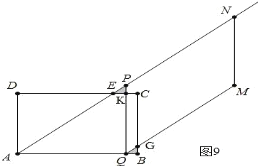
综上,t的值为2或3或![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
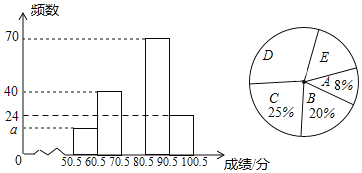
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发之后,全国许多省市对湖北各地进行了援助,广州市某医疗队备好医疗防护物资迅速援助武汉.第一批医疗队员乘坐高铁从广州出发,2.5小时后,第二批医疗队员乘坐飞机从广州出发,两批队员刚好同时到达武汉.已知广州到武汉的飞行距离为800千米,高铁路程为飞行距离的![]() 倍.
倍.
(1)求广州到武汉的高铁路程;
(2)若飞机速度与高铁速度之比为5:2,求飞机和高铁的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
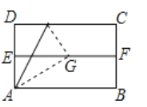
【题目】如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,已知BC=2,则线段EG的长度为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是( )
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
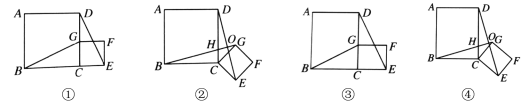
【题目】(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图④,若AB=a,BC=b;CE =ka,CG=kb,(
,如图④,若AB=a,BC=b;CE =ka,CG=kb,(![]() )试判断(1)中的结论是否仍然成立?并说明理由.
)试判断(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com