练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．在一次知识竞赛中，共有16道选择题，评分办法是：答对一题目得6分，答错一题扣2分，不答则不得分也不扣分，得分超过60为合格，明明有两道题未答，问他要达到合格，至少应答对几道题．（　　）
    A．9B．10C．11D．12

    分析 找到关键描述语，进而找到所求的量的等量关系．得到不等式6x-2（14-x）＞60，求解即可．

    解答 解：设答对x道．
    故6x-2（14-x）＞60
    解得：x＞11，所以至少要答对12道题，成绩才能在60分以上，
    故选D

    点评 本题考查一元一次不等式组的应用，将现实生活中的事件与数学思想联系起来，读懂题列出不等式关系式即可求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．已知3×9m×81m=325，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在象棋比寒中：胜方得1分，负方得0分，和棋双方均得0.5分，芳芳在第11盘结束后，积分领先，获得第一，其积分比甜甜的3倍多1分，求两人的积分是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程：-5x2+12x+32=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．某公司实行年工资制，职工的年工资由基础工资、住房补贴和医疗费三项组成，具体规定如下：
    项目第一年的工资（万元）一年后的计算方法
    基础工资1每年的增长率相同
    住房补贴0.04第二、三年比第一年增长4%、8%
    医疗费0.1384固定不变
    （1）设基础工资每年的增长率为x，用含x的代数式表示第三年的基础工资，为（1+x）2万元；
    （2）某人在公司工作了3年，他算了一下这3年拿到的住房补贴和医疗费正好是第3年基础工资的36%，问基础工资每年的增长率是多少？
    （$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{6}$≈2.450）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

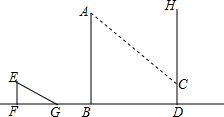    7．如图，一根长2m的木棒EF在地面上的影子FG为3m，此时15m高的旗杆AB的影子有一部分恰好落在16m的墙DH上，求旗杆的影子在墙上的高CD的长是多少？（精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

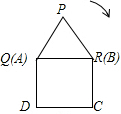    14．如图，如果边长为1的等边△PQR沿着边长为1的正方形ABCD的外部的边如图位置开始顺时针连续滚动，当它滚动4次时，点P所经过的路程是$\frac{7}{2}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．阅读理解应用 
       待定系数法：设某一多项式的全部或部分系数为未知数、利用当两个多项式为恒等式时，同类项系数相等的原理确定这些系数，从而得到待求的值．
       待定系数法可以应用到因式分解中，例如问题：因式分解x3-1．
       因为x3-1为三次多项式，若能因式分解，则可以分解成一个一次多项式和一个二次多项式的乘积．
       故我们可以猜想x3-1可以分解成x3-1=（x-1）（x2+ax+b），展开等式右边得：x3+（a-1）x2+（b-a）x-b，根据待定系数法原理，等式两边多项式的同类项的对应系数相等：a-1=0，b-a=0，-b=-1，可以求出a=1，b=1．
       所以x3-1=（x-1）（x2+x+1）
    （1）若x取任意值，等式x2+2x+3=x2+（3-a）x+s恒成立，则a=1；
    （2）已知多项式x4+x2+1有因式x2+x+1，请用待定系数法求出该多项式的另一因式．
    （3）请判断多项式x4-x2+1是否能分解成的两个整系数二次多项式的乘积，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）2+$\sqrt{b-2}$=0，过C作CB⊥x轴于B．
    （1）求三角形ABC的面积：
    （2）在y轴上是否存在点P，使得三角形ABC的面积和三角形ACP的面积相等？若存在，求出点P的坐标；若不存在，请说明理由：
    （3）如图2，在直线AC上有一点Q（6，m），在x轴上有两动点M（c，0）、N（c+1，0），当四边形QCMN的周长最小时，求M、N的坐标．

    查看答案和解析>>

    同步练习册答案