
【题目】在△ABC和△DEF中,下列条件不能判断这两个三角形全等的是( )
A.AB=DE,AC=DF,∠A=∠DB.∠A=∠D,∠B=∠E,AB=DE
C.AC=DF,BC=EF,∠B=∠ED.AB=DE,AC=DF,BC=EF
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.请根据以上信息回答:
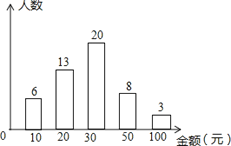
(1)该班同学所抢红包金额的众数是______,
中位数是______;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”
(1)下列分式中, 是和谐分式(填序号即可)
①![]() ②
②![]() ③
③![]() ④
④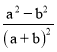
(2)若![]() 为正整数,且
为正整数,且![]() 为和谐分式,请写出所有
为和谐分式,请写出所有![]() 的值
的值
(3)在化简![]() 时,
时,
小强进行了如下三步变形:
原式=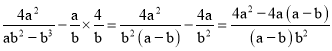
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | |
A村(元/辆) | B村(元/辆) | |
大货车 | ||
800 | 900 | |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+![]() 与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
A. 这两个函数图象有相同的对称轴 B. 这两个函数图象的开口方向相反
C. 方程-x2+k=0没有实数根 D. 二次函数y=-x2+k的最大值为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区环保局在检查该地区某铝厂时发现,该厂污水严重影响周围环境,要求做定期整改,据估测,该厂年排放污水量为36万吨,接到通知后,该厂决定分两期投入治理,一方面对排放的污水进行处理,同时使得处理后的污水年排放量减少到17.64万吨,如果每期治理中污水减少的百分率相同.
(1)问每期减少的百分率为多少?
(2)如果第一期治理中每减少排放1万吨污水,需投入2万元,第二期每减少排放1万吨污水,需投入3万元,问预计两期治理共需多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③4a-2b+c<0.其中正确的有( )

A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 图象于点A;MD⊥y轴于点D,交y=
图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com