
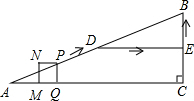
 如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).分析 (1)根据路程=速度×时间即可解决.
(2)分两种情形讨论①点N与D重合时,②点N落在线段DB上时分别求解即可.
(3)分5种情形讨论即可:①当0≤t≤2时,如图2中,②当2<t≤8时,如图3中,S=S正方形PQMN-S△DNK③当8<t≤10时,④当10<t≤$\frac{76}{7}$时,如图4中,S=PC2,
⑤当$\frac{76}{7}$<t≤16时,S=S正方形MNPQ-S△NKH分别求解即可.
(4)有4次相遇,分别列出方程求解即可.
解答 解:(1)∵在Rt△ABC中,AC=16,BC=12,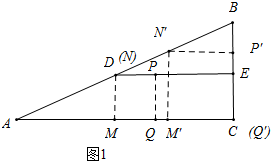
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=20,
∵点D为AB中点,
∴AD=10,
∴点P在AD段的运动时间为$\frac{10}{5}$=2s;
∴当点P在线段DE上运动时,DP段的运动时间为(t-2)s,
∵DE段运动速度为1,
∴DP=(t-2)cm;
故答案为t-2.
(2)如图1中,点N与D重合时,∵PQ=EC=PN=6,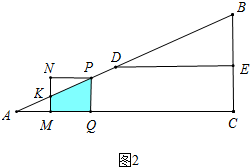
∴点P运动时间t=2+6=8秒,
点N落在线段DB上时,设P′N′=x,
∵P′N′∥AC,
∴$\frac{P′N′}{AC}$=$\frac{BP′}{BC}$,
∴$\frac{x}{16}$=$\frac{12-x}{12}$,
∴x=$\frac{48}{7}$,
∴P′E=$\frac{6}{7}$,
∴点P运动时间t=2+8+$\frac{6}{7}$=$\frac{76}{7}$秒.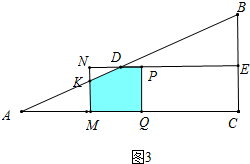
(3)如图2中,①当0≤t≤2时,∵KM∥PQ,
∴$\frac{KM}{PQ}$=$\frac{AM}{AQ}$,
∴$\frac{KM}{3t}$=$\frac{t}{4t}$,
∴KM=$\frac{3}{4}$t,
∴S=S△APQ-S△AKM=$\frac{1}{2}$•4t•3t-$\frac{1}{2}$•t•$\frac{3}{4}$t=$\frac{45}{8}$t2.
②当2<t≤8时,如图3中,
S=S正方形PQMN-S△DNK=36-$\frac{1}{2}$•(6-$\frac{3}{4}$t)•[6-(t-2)]=-$\frac{3}{8}$t2+6t+12.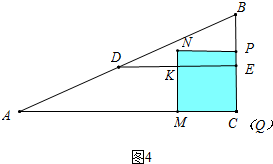
③当8<t≤10时,S=36,
④当10<t≤$\frac{76}{7}$时,如图4中,S=PC2=[6+(t-10)]2=t2-8t+16.
⑤当$\frac{76}{7}$<t≤16时,如图5中,
∵PH∥AC,
∴$\frac{PH}{AC}$=$\frac{BP}{BC}$,
∴$\frac{PH}{16}$=$\frac{6-(t-10)}{12}$,
∴PH=$\frac{4}{3}$(16-t),
∴NH=(6+(t-10)-$\frac{4}{3}$(16-t)=$\frac{7}{3}$t-$\frac{76}{3}$,
∴NK=$\frac{3}{4}$NH=$\frac{7}{4}$t-19,
∴S=S正方形MNPQ-S△NKH=(t-4)2-$\frac{1}{2}$•($\frac{7}{4}$t-19)($\frac{7}{3}$t-$\frac{76}{3}$)=-$\frac{25}{24}$t2+$\frac{109}{7}$t-$\frac{674}{7}$. 综上所述S=$\left\{\begin{array}{l}{\frac{45}{8}{t}^{2}}&{(0<t≤2)}\\{-\frac{3}{8}{t}^{2}+^t+12}&{(2<t≤8)}\\{36}&{(8<t≤10)}\\{{t}^{2}-8t+16}&{(10<t≤\frac{76}{7})}\\{-\frac{25}{24}{t}^{2}+\frac{109}{7}t-\frac{674}{7}}&{(\frac{76}{7}<t≤16)}\end{array}\right.$.
综上所述S=$\left\{\begin{array}{l}{\frac{45}{8}{t}^{2}}&{(0<t≤2)}\\{-\frac{3}{8}{t}^{2}+^t+12}&{(2<t≤8)}\\{36}&{(8<t≤10)}\\{{t}^{2}-8t+16}&{(10<t≤\frac{76}{7})}\\{-\frac{25}{24}{t}^{2}+\frac{109}{7}t-\frac{674}{7}}&{(\frac{76}{7}<t≤16)}\end{array}\right.$.
(4)第一次相遇由题意:$\frac{6(t-8)}{8-(t-8)}=\frac{3}{4}$,解得t=$\frac{80}{9}$,
第二次相遇由题意:$\frac{6(t-8)-6}{t-8}$=$\frac{3}{4}$,解得t=$\frac{64}{7}$.
第三次相遇由题意:$\frac{6(t-8)-12}{t-4}$=$\frac{3}{4}$,解得t=$\frac{76}{7}$.
第四次相遇由题意:$\frac{t-4-[6(t-8)12-(t-4)]}{t-4}$=$\frac{3}{4}$,解得t=$\frac{220}{19}$.
∴点P的整个运动过程中,点H落在线段CD上时t的值为$\frac{80}{9}$秒或$\frac{64}{7}$秒或$\frac{76}{7}$秒或$\frac{220}{19}$秒.
点评 本题考查相似综合题、正方形的性质、相似三角形的性质平行线分线段成比例定理等知识,解题的关键是正确画出图形,确定自变量的取值范围,本题计算量大,比较难,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:
某校对七、八、九年级的学生进行体育水平测试,成绩评定为优秀、良好、合格、不合格四个等第.为了解这次测试情况,学校从三个年级随机抽取200名学生的体育成绩进行统计分析.相关数据的统计图、表如下:| 各年级学生成绩统计表 | ||||
| 优秀 | 良好 | 合格 | 不合格 | |
| 七年级 | a | 20 | 24 | 8 |
| 八年级 | 29 | 13 | 13 | 5 |
| 九年级 | 24 | b | 14 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com