
△ABC中,AB=AC,D为BC的中点,以D为顶点作∠MDN=∠B.
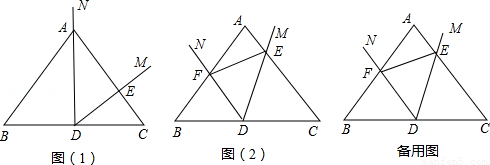
(1)如图(1)当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似的三角形.
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF的面积等于△ABC的面积的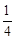 时,求线段EF的长.
时,求线段EF的长.
(1)△ABD,△ACD,△DCE(2)△BDF∽△CED∽△DEF,证明见解析
【解析】解:(1)图(1)中与△ADE相似的有△ABD,△ACD,△DCE。(3)5
(2)△BDF∽△CED∽△DEF,证明如下:
∵∠B+∠BDF+∠BFD=180°,∠EDF+∠BDF+∠CDE=180°,
又∵∠EDF=∠B,∴∠BFD=∠CDE。
∵AB=AC,∴∠B=∠C。∴△BDF∽△CED。∴ 。
。
∵BD=CD,∴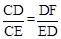 ,即
,即 。
。
又∵∠C=∠EDF,∴△CED∽△DEF。∴△BDF∽△CED∽△DEF。
(3)连接AD,过D点作DG⊥EF,DH⊥BF,垂足分别为G,H.

∵AB=AC,D是BC的中点,∴AD⊥BC,BD= BC=6。
BC=6。
在Rt△ABD中,AD2=AB2﹣BD2,即AD2=102﹣62,
∴AD=8。
∴S△ABC= •BC•AD=
•BC•AD= ×12×8=48,
×12×8=48,
S△DEF= S△ABC=
S△ABC= ×48=12。
×48=12。
又∵ •AD•BD=
•AD•BD= •AB•DH,∴
•AB•DH,∴ 。
。
∵△BDF∽△DEF,∴∠DFB=∠EFD。
∵DH⊥BF,DG⊥EF,∴∠DHF=∠DGF。
又∵DF=DF,∴△DHF≌△DGF(AAS)。∴DH=DG= 。
。
∵S△DEF= ·EF·DG=
·EF·DG= ·EF·
·EF· =12,∴EF=5。
=12,∴EF=5。
(1)根据等腰三角形的性质以及相似三角形的判定得出△ADE∽△ABD∽△ACD∽△DCE:
∵AB=AC,D为BC的中点,∴AD⊥BC,∠B=∠C,∠BAD=∠CAD。
又∵∠MDN=∠B,∴△ADE∽ABD。
同理可得:△ADE∽△ACD。
∵∠MDN=∠C=∠B,∠B+∠BAD=90°,∠ADE+∠EDC=90°,∠B=∠MDN,
∴∠BAD=∠EDC。
∵∠B=∠C,∴△ABD∽△DCE。∴△ADE∽△DCE。
(2)利用已知首先求出∠BFD=∠CDE,即可得出△BDF∽△CED,再利用相似三角形的性质得出 ,从而得出△BDF∽△CED∽△DEF。
,从而得出△BDF∽△CED∽△DEF。
(3)利用△DEF的面积等于△ABC的面积的 ,求出DH的长,从而利用S△DEF的值求出EF即可
,求出DH的长,从而利用S△DEF的值求出EF即可


科目:初中数学 来源: 题型:
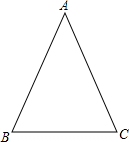 如图,在△ABC中,AB=AC,∠A=36°,
如图,在△ABC中,AB=AC,∠A=36°,| CD | DA |
查看答案和解析>>
科目:初中数学 来源: 题型:
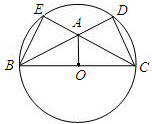 ,连接AO、BE、DC.
,连接AO、BE、DC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com