
 如下图,直角梯形ABCD中,AD∥BC,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动、P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts.
如下图,直角梯形ABCD中,AD∥BC,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动、P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts. 解:(1)∵PD∥CQ,∴当PD=CQ时,四边形PQCD是平行四边形.
解:(1)∵PD∥CQ,∴当PD=CQ时,四边形PQCD是平行四边形.

 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
如下图所示,在直角梯形ABCD中,AB∥CD,∠A=90°,点E为AD的中点,P在腰BC上且不与B,C重合,连接PD,PE,AB=18,CD=6,AD=16,设PC=x,S△PDE=y.

(1)求y与x之间的函数关系式;
(2)x为何值时,tan∠DPE=![]() ?
?
(3)是否存在x,使S△DPC=![]() S梯形ABCD?
S梯形ABCD?
查看答案和解析>>
科目:初中数学 来源: 题型:013
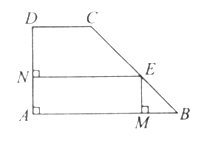
如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM上AB于M,EN垂直于AD于N,设BM=x,矩形AMEN的面积为y,那么y与x之间的函数关系的图象大致是下图中的( ).

查看答案和解析>>
科目:初中数学 来源:2009年重庆市中考数学试卷 题型:044
已知:如下图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.

(1)求证:BG=FG;
(2)若AD=DC=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
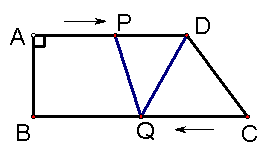
如下图,直角梯形ABCD中,AD∥BC, AB=![]() cm,AD=24
cm,AD=24![]() ,BC=26
,BC=26![]() ,∠B=90°,动点P从A开始沿AD边向D以1
,∠B=90°,动点P从A开始沿AD边向D以1![]() 的速度运动,动点Q从点C开始沿CB以3
的速度运动,动点Q从点C开始沿CB以3![]() 的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为
的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为![]() ,
,
问:(1)![]() = 时,四边形PQCD是平行四边形.
= 时,四边形PQCD是平行四边形.
(2)是否存在一个t值,使PQ把梯形ABCD分成面积相等的两部分,若存在请求出t的值.
(3)当![]() 为何值时,四边形PQCD为等腰梯形.
为何值时,四边形PQCD为等腰梯形.
(4)连接DQ,是否存在![]() 值使△CDQ为等要三角形,若存在请直接写出
值使△CDQ为等要三角形,若存在请直接写出![]() 的值.
的值.
 |
查看答案和解析>>
科目:初中数学 来源:湖北省月考题 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com