
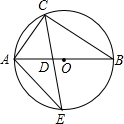
 如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )
如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于点E,∠E=30°,交AB于点D,连接AE,则SADC:S△ADE的比值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
分析 过C作CF⊥AB于F,连接OE,设AC=a,求出CF,OE,根据S△ADC:S△ADE=$\frac{1}{2}$•AD•CF:$\frac{1}{2}$•AD•OE计算即可.
解答 解:过C作CF⊥AB于F,连接OE,设AC=a,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=∠E=30°,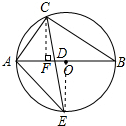
∴∠A=60°,∠ACF=30°,CF=$\frac{\sqrt{3}}{2}$a,AB=2AC=2a,
∵CE平分∠ACB交⊙O于E,
∴$\widehat{AE}$=$\widehat{BE}$,
∴OE⊥AB,
∴OE=$\frac{1}{2}$AB=a
∴S△ADC:S△ADE=$\frac{1}{2}$•AD•CF:$\frac{1}{2}$•AD•OE=$\sqrt{3}$:2.
故选C.
点评 本题考查了圆周角定理,三角形的角平分线定理,三角形的面积的计算,直角三角形的性质,正确作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
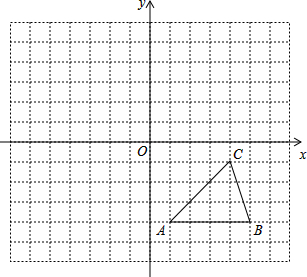 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{c}=\frac{d}{b}$ | B. | $\frac{c}{a}=\frac{ac}{bd}$ | C. | $\frac{a+2b}{b}=\frac{c+2d}{d}$ | D. | $\frac{a+1}{b}=\frac{c+1}{d}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
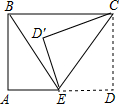 如图,四边形ABCD,AD∥BC,∠A=∠D=90°,E为AD中点,将点D绕着CE翻折到点D’处,连接BE,记∠AED’=α,∠ABE=β,则α与β之间的数量关系为( )
如图,四边形ABCD,AD∥BC,∠A=∠D=90°,E为AD中点,将点D绕着CE翻折到点D’处,连接BE,记∠AED’=α,∠ABE=β,则α与β之间的数量关系为( )| A. | α=β | B. | α=2β | C. | α+β=90° | D. | α+2β=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
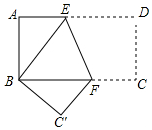 长方形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF.
长方形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com