
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,OE⊥OD.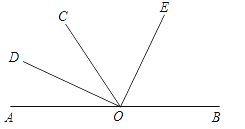
(1)求∠BOD的度数;
(2)请通过计算说明OE是否平分∠BOC.
【答案】
(1)解:∵OD平分∠AOC
∴∠AOD=∠DOC= ![]() ∠AOC=
∠AOC= ![]() ×50°=25°,
×50°=25°,
∴∠BOD=180°﹣∠AOD=180°﹣25°=155°
(2)解:∵OE⊥OD,∴∠DOE=90°,
∵∠DOC=25°,
∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°,
∵∠BOD=155°,∠DOE=90°,
∴∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
∴∠COE=∠BOE,即OE平分∠BOC
【解析】(1)根据角平分线的定义及∠AOC的度数求出∠AOD的度数,再根据邻补角的定义由∠BOD=180°﹣∠AOD,计算得出答案即可。
(2)根据垂直的定义得出∠DOE=90°,再根据∠COE=∠DOE﹣∠DOC,∠BOE=∠BOD﹣∠DOE,分别求出∠COE和∠BOE的度数,就可判断两角是否相等,若相等则OE是平分∠BOC,反之OE不平分∠BOC。


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;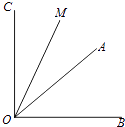
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
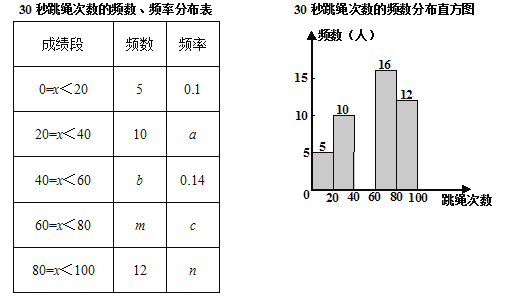
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB、CD交于点O,OE⊥AB于O,则下列不正确的是( ) 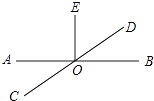
A.∠AOC与∠BOD是对顶角
B.∠BOD和∠DOE互为余角
C.∠AOC和∠DOE互为余角
D.∠AOE和∠BOC是对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为 . 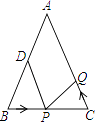
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com