练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．观察下面的点阵图，探究其中的规律．
    摆第1个“小屋子”需要5个点，
    摆第2个“小屋子”需要11个点，摆第3个“小屋子”需要17个点？
    （1）、摆第10个这样的“小屋子”需要多少个点？
    （2）、写出摆第n个这样的“小屋子”需要的总点数，S与n的关系式．

    分析 （1）通过观察已知图形可以将“小屋子”分为屋顶和屋身两部分，屋顶的点的个数分别是1、3、5、7、…，即第n个小屋子的屋顶点的个数是2n-1；屋身的点的个数分别是4、8、12、…，据此可得；
    （2）第n个图形的屋身是4n个；所以第n个小屋子共有6n-1，即可求出答案．

    解答 解：摆第1个“小屋子”需要5枚棋子，
    摆第2个需要3+4×2=11枚棋子，
    摆第3个需5+4×3=17枚棋子，
    故答案为：11、17；

    （1）摆第10个这样的“小屋子”需要2×10-1+4×10=59个点；

    （2）按这种方式摆下去，摆第n个这样的“小屋子”需要2n-1+4n=6n-1枚棋子．

    点评 本题考查了图形的变化类问题，关键是通过归纳与总结，得到其中的规律．注意由特殊到一般的分析方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图所示，在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3），直线m为横坐标都为2的点组成的一条直线，作出△ABC关于直线m对称的△A1B1C1，并直接写出A1，B1，C1的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

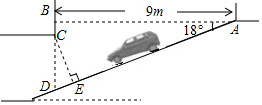    18．为缓解“停车难”的问题，某单位拟造地下停车库，建筑设计师提供了该地下停车库的设计示意图如图所示，已知该坡道的水平距离AB的长为9m，坡面AD与AB的夹角∠BAD=18°，石柱BC=0.5m，按规定，地下停车库坡道上方BC处要张贴限高标志，以便告知停车人车辆能否安全驶入．请你帮设计师计算一下CE的高度，以便张贴限高标志，结果精确到0.1m．
    （参考数值：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，AD∥BC，∠CDE=∠E，试判断∠A与∠C之间的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，直线AB⊥CD，垂足为O，直线EF经过点O，∠1=30°，求∠AOF、∠AOE和∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．赵明是一名健步走运动的爱好者，他用手机软件记录了某天“健步团队”中每一名成员健步走的步数（单位：千步，横轴上每组数据包含最小值不包含最大值）．随机调查了其中部分成员，将被调查成员每天健步走步数x（单位：千步）进行了统计，根据所得数据绘制了如下两个统计图，请根据所给信息，解答下列问题：

    （1）本次调查属于抽样调查，样本容量是50．
    （2）请补全频数分布直方图中空缺的部分．
    （3）被调查的成员每天健步走步数的中位数落在B组．
    （4）若该团队共有200人，请估计每天健步走步数不少于8.0千步的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．（1）解不等式$\frac{x-2}{2}$≥$\frac{7-x}{3}$并把它的解集表示在数轴上．
    （2）$\left\{\begin{array}{l}{3x-2＜x+1①}\\{x+5＞4x+1②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．“母亲节”前夕，一花店用3000元购进若干束花，很快售完，接着又用7500元购进第二批花，已知第二批所购花束的数量是第一批所购花束的2倍，且每束花的进价比第一批的进价多5元．
    （1）求第一批花每束的进价是多少元？
    （2）第一批花售价为30元，如果要两批花全部售完后盈利不少于6000元，则第二批花售价至少是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

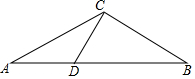    17．如图，在△ABC中，∠A=30°，D为边AB上的点，且DA=DC=2，若△DCB绕点D逆时针旋转，使DB、DC分别与线段AC相交于M、N，则当△DMN为等边三角形时，DM的长值为$\frac{2\sqrt{3}}{3}$．

    查看答案和解析>>

    同步练习册答案