
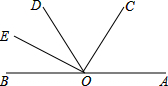
 如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.
如图,已知AOB是一条直线,OC是∠AOD 的平分线,OE是∠BOD的平分线.分析 (1)由角平分线的定义,可求得∠COE,再利用角的和差可求得∠AOC;
(2)利用(1)中所求∠COE,再结合条件可求得∠COD.
解答 解:
(1)∵OC是∠AOD 的平分线,OE是∠BOD的平分线,
∴∠DOE=$\frac{1}{2}$∠BOD,∠COD=$\frac{1}{2}$∠AOD,
∵AOB是一条直线,
∴∠AOB=180°,
∴∠COE=∠DOE+∠COD=$\frac{1}{2}$∠BOD+$\frac{1}{2}$∠AOD=$\frac{1}{2}$(∠BOD+∠AOD)=$\frac{1}{2}$∠AOB=90°,
∴∠AOC=∠AOE-∠EOC=140°-90°=50°;
(2)由(1)可知∠EOC=90°,
∵∠EOD:∠COD=2:3,
∴可设∠EOD=2x°,∠COD=3x°,
∴2x+3x=90,解得x=18,
∴∠COD=3x°=54°.
点评 本题主要考查角平分线的定义,掌握角平分线把已知角分成两个相等的角是解题的关键.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
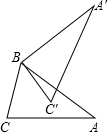 如图,在△ABC中,AB=AC,将△ABC绕B点逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′度数为( )
如图,在△ABC中,AB=AC,将△ABC绕B点逆时针方向旋转60°,得到△A′BC′,若A′C′⊥AB,则∠ABC′度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
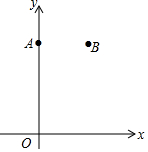 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com