
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
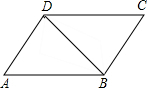 如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.
如图,已知AD∥CB,∠A=∠C,若∠ABD=32°,求∠BDC的度数.有同学用了下面的方法.但由于一时犯急没有写完整,请你帮他添写完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
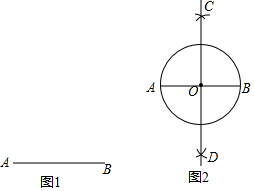 下面是“以已知线段为直径作圆”的尺规作图过程.
下面是“以已知线段为直径作圆”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=(m+2)x2-2(m+2)x-m+5,其中m+2>0.
二次函数y=(m+2)x2-2(m+2)x-m+5,其中m+2>0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
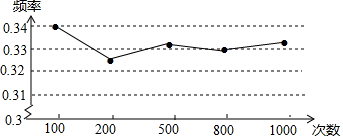
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.
有这样一个问题:探究函数y=$\frac{{x}^{2}}{2x-2}$的图象与性质.| x | … | -3 | -2 | -1 | 0 | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{9}{8}$ | -$\frac{2}{3}$ | -$\frac{1}{4}$ | 0 | 2 | $\frac{9}{4}$ | $\frac{8}{3}$ | $\frac{25}{8}$ | … |
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )
A. 45×103 B. 4.5×104 . C. 4.5×105. D. 0.45×105.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com