练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．满足不等式5（x-1）＞1+x的最小整数解是2．

    分析 首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的最小整数解即可．

    解答 解：不等式的解集是x＞$\frac{3}{2}$，
    故不等式5（x-1）＞1+x的最小整数解为2．
    故答案为；2．

    点评 本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．在四边形ABCD中，AB=BC=CD=DA，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是（　　）
    A．AC⊥BDB．AB∥CDC．∠A=90°D．∠A=∠C

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列各曲线表示的y与x的关系中，y不是x的函数的是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

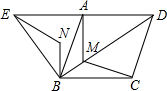    12．如图，四边形ABCD是菱形，且∠ABC=60°，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
    （1）求证：△EBN≌△ABM；
    （2）当M点在何处时，AM+BM+CM的值最小？请说明理由．
    （3）在（2）的条件下，以B为原点，BC为x轴正方向建立直角坐标系，若菱形ABCD的边长为2，求M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    （1）$\sqrt{48}$$÷\sqrt{3}$$-\sqrt{\frac{1}{2}}$×$\sqrt{12}$
    （2）（3-$\sqrt{3}$）（1+$\frac{1}{\sqrt{3}}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．实数a，b在数轴上的位置如图所示，则化简$\sqrt{（a-b）^{2}}$-$\sqrt{（1-a）^{2}}$-$\sqrt{{b}^{2}}$结果是（　　）
    A．-2a-1B．-1C．2b-1D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在某项针对18～35岁的青年人每天发微博数量的调查中，设一个人的“日均发微博条数”为m，规定：当0≤m≤5时为A级，5≤m＜10时为B级，10≤m＜15时为C级，15≤m＜20时为D级．现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查，根据调查数据整理并制作图表如下：
    请你根据以上信息解答下列问题：
    （1）在表中：a=300，b=60；
    （2）补全频数分布直方图；
    （3）若北京市常住人口中18～35岁的青年人大约有530万人，试估计其中“日均发微博条数”不少于10条的大约有多少万人．
    m频数百分数
    A级（0≤m≤5）90          0.3
    B级（5≤m＜10）120          a
    C级（10≤m＜15）b           0.2
    D级（15≤m＜20）30           0.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，∠B=30°，∠C=70°，AD平分∠BAC，交BC于F，DE⊥BC于E，则∠D=20°．

    查看答案和解析>>

    同步练习册答案