
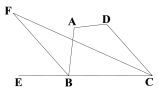
【题目】如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)若BF∥CD,∠ABC=80°,求∠DCB的度数;
(2)已知四边形ABCD中,∠A=105,∠D=125,求∠F的度数;
(3)猜想∠F、∠A、∠D之间的数量关系,并说明理由.
【答案】(1)50°;(2)25°;(3)∠F=(∠A+∠D-180)°.
【解析】
(1)由∠ABC=80°,可知∠ABE=100°,根据BF平分∠ABE,BF∥CD可得∠BCD=50°.
(2)由三角形外角性质可知∠F=∠FBE-∠FCE,而BF平分∠ABE、CF平分∠BCD,故∠F=![]() (∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(∠ABE-∠FCE),由补角性质和四边形内角和可得∠ABE=360°-∠A-∠B-∠BCD,将已知代入即可求解;
(3)同(2)可得∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
解:(1)∵∠ABC=80°,
∴∠ABE=180°-∠ABC=100°,
∵BF平分∠ABE,
∴∠EBF=![]() ∠ABE=50°,
∠ABE=50°,
∵BF∥CD
∴∠BCD=∠EBF=50°;
(2)∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),
∵∠A=105,∠D=125,
∴∠F=![]() (105 +125 -180°)=25°,
(105 +125 -180°)=25°,
(3)结论:∠F=![]() (∠A+∠D-180°)
(∠A+∠D-180°)
理由如下:∵∠FBE是△EBC的外角,
∴∠F=∠EBF-∠ECF
∵BF平分∠ABE、CF平分∠BCD,
∴∠EBF=![]() ∠ABE=,∠ECF=
∠ABE=,∠ECF=![]() ∠BCD,
∠BCD,
∵∠ABE=180°-∠ABC,
∴∠F=![]() (180°-∠ABC)-
(180°-∠ABC)-![]() ∠BCD=
∠BCD=![]() [180°-(∠ABC+∠BCD)],
[180°-(∠ABC+∠BCD)],
∵在四边形ABCD中,∠ABC+∠BCD=360°-∠A-∠D,
∴∠F=![]() [180°-(360°-∠A-∠D)],
[180°-(360°-∠A-∠D)],
∴∠F=![]() (∠A+∠D-180°),
(∠A+∠D-180°),


科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,AB是弦,PA∥BC交AB于点D.
(1)求证:PB是⊙O的切线.
(2)当BC=2 ![]() ,cos∠AOD=
,cos∠AOD= ![]() 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
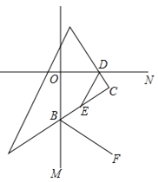
【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图,若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元.
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂购买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于400个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2﹣4ac>0中错误的个数为( )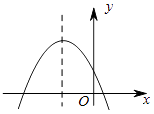
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.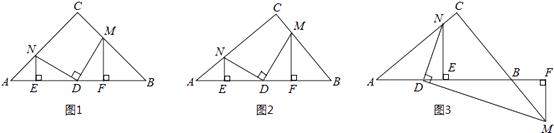
(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;
(2)拓展探究:若AC≠BC.
①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;
②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE与DF的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com