
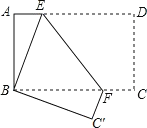
【题目】如图,长方形纸片 ABCD,AD∥BC,将长方形纸片折叠, 使点 D 与点 B 重合,点 C 落在点 C'处,折痕为 EF.
(1)求证:BE=BF.
(2)若∠ABE=18°,求∠BFE 的度数.
(3)若 AB=4,AD=8,求 AE 的长.
【答案】(1)详见解析;(2)57°;(3)3.
【解析】
(1)根据翻折变换的性质,结合矩形的性质证明∠BEF=∠BFE,根据等腰三角形的判定即可得到结论;
(2)根据矩形的性质及等腰三角形的性质即可解决问题;
(3)根据勾股定理列出关于线段 AE 的方程即可解决问题;
解:(1)由题意得:∠BEF=∠DEF;
∵四边形 ABCD 为矩形,
∴DE∥BF,
∴∠BFE=∠DEF,
∴∠BEF=∠BFE,
∴BE=BF;
(2)∵四边形 ABCD 为矩形,
∴∠ABF=90°;而∠ABE=24°,
∴∠EBF=90°-24°=66° ;
又∵BE=BF,
∴∠BFE =![]() =57°;
=57°;
(3)由题意知:BE=DE;
设 E=x,则 BE=DE=8-x,
由勾股定理得:(8-x)2=42+x2,解得:x=3.
即 AE 的长为 3.


科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )

A. 16张 B. 18张 C. 20张 D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(﹣1,0)、B(0,2)、C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A',则A'C的最小值为( )
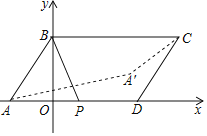
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
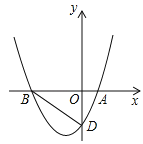
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.
(1)求抛物线的解析式;
(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,四边形PBQD能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;
(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从点A看一山坡上的电线杆PQ,观测杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度(精确到0.1 m).
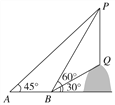
查看答案和解析>>
科目:初中数学 来源: 题型:
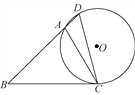
【题目】如图,在△ABC中,∠B=45°,∠ACB=60°,AB=3![]() ,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
,D为BA延长线上的一点,且∠D=∠ACB,⊙O为△ACD的外接圆.
(1)求BC的长;
(2)求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:
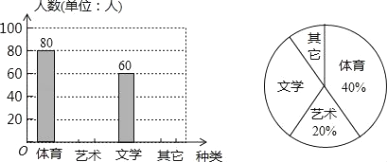
(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com