
 如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.
如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$. 分析 作点B关于直线AC的对称点K,连接AK、CK,作点N关于直线AC的对称点N′,作N′P′⊥BC于P′,交AC于M′,则线段N′P′的长即为PM+MN的最小值(垂线段最短).
解答 解:作点B关于直线AC的对称点K,连接AK、CK,作点N关于直线AC的对称点N′,作N′P′⊥BC于P′,交AC于M′,则线段N′P′的长即为PM+MN的最小值(垂线段最短).
∵△ABC是等边三角形,易知,四边形ABCK是菱形,N′P′是菱形的高=$\frac{\sqrt{3}}{2}$×4=2$\sqrt{3}$,
∴PM+MN的最小值为2$\sqrt{3}$,
故答案为2$\sqrt{3}$.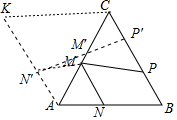
点评 本题考查轴对称最短问题、等边三角形的性质、垂线段最短等知识,解题的关键是学会添加辅助线,利用对称,根据垂线段最短解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | a2+b>0 | B. | a-b>0 | C. | a2-b>0 | D. | a+b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
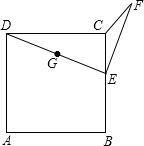 如图,已知正方形ABCD的边长为10,E在BC边上运动,取DE的中点G,EG绕点E顺时针旋转90°得EF,问CE长为多少时,A、C、F三点在一条直线上( )
如图,已知正方形ABCD的边长为10,E在BC边上运动,取DE的中点G,EG绕点E顺时针旋转90°得EF,问CE长为多少时,A、C、F三点在一条直线上( )| A. | $\frac{8}{3}$ | B. | $\frac{6}{5}$ | C. | $\frac{10}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
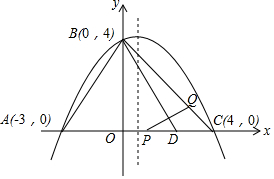 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com