
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

【答案】(1)证明见解析(2)![]()
【解析】
(1)由点G是AE的中点,根据垂径定理可知OD⊥AE,由等腰三角形的性质可得∠CBF=∠DFG,∠D=∠OBD,从而∠OBD+∠CBF=90°,从而可证结论;
(2)连接AD,解Rt△OAG可求出OG=3,AG=4,进而可求出DG的长,再证明△DAG∽△FDG,由相似三角形的性质求出FG的长,再由勾股定理即可求出FD的长.
(1)∵点G是AE的中点,
∴OD⊥AE,
∵FC=BC,
∴∠CBF=∠CFB,
∵∠CFB=∠DFG,
∴∠CBF=∠DFG
∵OB=OD,
∴∠D=∠OBD,
∵∠D+∠DFG=90°,
∴∠OBD+∠CBF=90°
即∠ABC=90°
∵OB是⊙O的半径,
∴BC是⊙O的切线;
(2)连接AD,

∵OA=5,tanA=![]() ,
,
∴OG=3,AG=4,
∴DG=OD﹣OG=2,
∵AB是⊙O的直径,
∴∠ADF=90°,
∵∠DAG+∠ADG=90°,∠ADG+∠FDG=90°
∴∠DAG=∠FDG,
∴△DAG∽△FDG,
∴![]() ,
,
∴DG2=AGFG,
∴4=4FG,
∴FG=1
∴由勾股定理可知:FD=![]() .
.


科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
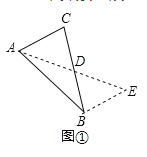

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.
x2+x+3的顶点为P,与y轴交于点A,若向右平移4个单位,向下平移4个单位,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应新中考英语听说机考,九年级甲、乙两位同学使用某手机软件进行英语听说练习并记录了40次的练习成绩.甲、乙两位同学的练习成绩统计结果如图所示:

下列说法正确的是( )
A. 甲同学的练习成绩的中位数是38分
B. 乙同学的练习成绩的众数是15分
C. 甲同学的练习成绩比乙同学的练习成绩更稳定
D. 甲同学的练习总成绩比乙同学的练习总成绩低
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx+3m﹣3,以下说法:①图象过定点(![]() ),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )
A. ①② B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com