
【题目】某商店购进甲乙两种商品,甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同.
(1)求甲、乙每个商品的进货单价;
(2)若甲、乙两种商品共进货100件,要求两种商品的进货总价不高于9000元,同时甲商品按进价提高10%后的价格销售,乙商品按进价提高25%后的价格销售,两种商品全部售完后的销售总额不低于10480元,问有哪几种进货方案?
(3)在条件(2)下,并且不再考虑其他因素,若甲乙两种商品全部售完,哪种方案利润最大?最大利润是多少?
【答案】(1)甲商品的单价是每件100元,乙每件80元;(2)有3种进货方案;(3)当甲进48件,乙进52件时,最大的利润是1520元.
【解析】
试题分析:(1)设甲每个商品的进货单价是x元,每个乙商品的进货单价是y元,根据“甲的进货单价比乙的进货单价高20元,已知20个甲商品的进货总价与25个乙商品的进货总价相同”列方程组,解方程组即可求解;(2)设甲进货x件,乙进货(100﹣x)件,根据两种商品的进货总价不高于9000元,两种商品全部售完后的销售总额不低于10480元即可列不等式组求解,即可确定方案;(3)找出销售利润与x的函数关系式,利用一次函数的性质即可求解.
试题解析:(1)设甲每个商品的进货单价是x元,每个乙商品的进货单价是y元.
根据题意得:![]() ,
,
解得:x=100,y=80,
答:甲商品的单价是每件100元,乙每件80元;
(2)设甲进货x件,乙进货(100﹣x)件.
根据题意得:![]() ,
,
解得:48≤x≤50.
又∵x是正整数,则x的正整数值是48或49或50,则有3种进货方案;
(3)销售的利润w=100×10%x+80(100﹣x)×25%,即w=2000﹣10x,
则当x取得最小值48时,w取得最大值,是2000﹣10×48=1520(元).
此时,乙进的件数是100﹣48=52(件).
答:当甲进48件,乙进52件时,最大的利润是1520元.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,在“4×4”正方形网格中,已有2个小正方形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).

(只有1条对称轴) (只有2条对称轴)
图⑴ 图⑵
⑵如图,A、B为直线MN外两点,且到MN的距离不相等.分别在MN上求一点P,并满足如下条件:①在图⑶中求一点P使得PA+PB最小; ②在图⑷中求一点P使得|PA-PB|最大.
(不写作法,保留作图痕迹)
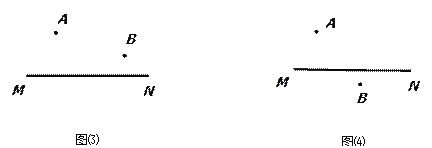
查看答案和解析>>
科目:初中数学 来源: 题型:
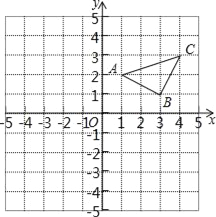
【题目】已知:如图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
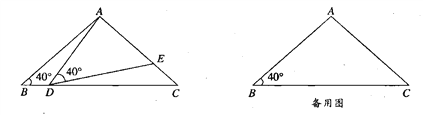
【题目】如图,在△ABC中,AB=AC=4,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;
(2)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求出∠BDA的度数.若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com