
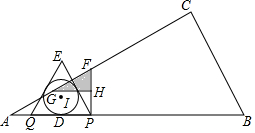
 ��ͼ����Rt��ABC�У���C=Rt�ϣ���A=30�㣬AB=10$\sqrt{3}$����D�ڱ�AB�ϣ�AD=2$\sqrt{3}$����P��Qͬʱ��ÿ��$\sqrt{3}$����λ���ٶȴ�D���������P��DB�����˶�����Q��DA����A��������ԭ�ٷ������B�˶�����PQΪ���������ȱߡ�PQE��������Բ��I����P��PF��AB������AC-CB�ڵ�F��FP�Ƶ�F˳ʱ����ת60��õ�FG����G��GH��FP��H����P�˶�����Bʱ��P��Qֹͣ�˶������˶�ʱ��Ϊt�룮
��ͼ����Rt��ABC�У���C=Rt�ϣ���A=30�㣬AB=10$\sqrt{3}$����D�ڱ�AB�ϣ�AD=2$\sqrt{3}$����P��Qͬʱ��ÿ��$\sqrt{3}$����λ���ٶȴ�D���������P��DB�����˶�����Q��DA����A��������ԭ�ٷ������B�˶�����PQΪ���������ȱߡ�PQE��������Բ��I����P��PF��AB������AC-CB�ڵ�F��FP�Ƶ�F˳ʱ����ת60��õ�FG����G��GH��FP��H����P�˶�����Bʱ��P��Qֹͣ�˶������˶�ʱ��Ϊt�룮���� ��1����֪��0��t��2ʱ��AP=2$\sqrt{3}$+$\sqrt{3}$t��AQ=2$\sqrt{3}$-$\sqrt{3}$t��
��2����ͼ1�У���CK��AB��K���������F��C�غ�ʱ��FG=FP=CK����ʱFG��ֵ������DK��ֵ���ɽ�����⣮
��3���ٷ������������a����ͼ2�У�����AI��IQ��ID������I��AC��AB����ʱ����IAD=��IAC=15�㣬��IQD=30�㣬�Ƴ���QAI=��QIA=15�㣬�Ƴ�AQ=IQ����ID=x����IQ=AQ=2x��DQ=$\sqrt{3}$x����AD=2$\sqrt{3}$���ɵ�2x+$\sqrt{3}$x=2$\sqrt{3}$���ⷽ�̼��ɣ�b����ͼ3�У���t��2ʱ����I��AC��AB����ʱ����취�г����̼��ɽ�����⣮C����ͼ4�У���P��B�غ�ʱ����I��AB��BC���У���ʱt=$\frac{8\sqrt{3}}{\sqrt{3}}$=8��
�����ͼ5��ͼ6��ͼ7��ͼ8�У�G�ڡ�I��ʱ��t��ֵ���ɽ�����⣮
��� �⣺��1����0��t��2ʱ��������AP=2$\sqrt{3}$+$\sqrt{3}$t��AQ=2$\sqrt{3}$-$\sqrt{3}$t��
�ʴ�Ϊ2$\sqrt{3}$+$\sqrt{3}$t��2$\sqrt{3}$-$\sqrt{3}$t��
��2����ͼ1�У���CK��AB��K��
��Rt��ACB�У���AB=10$\sqrt{3}$����A=30�㣬
��BC=5$\sqrt{3}$��AC=$\sqrt{3}$BC=15��
��Rt��ACK�У���AC=15����A=30�㣬
��CK=$\frac{15}{2}$��AK=$\sqrt{3}$CK=$\frac{15}{2}$$\sqrt{3}$��
��AD=2$\sqrt{3}$��
��DK=AK-AD=$\frac{11}{2}$$\sqrt{3}$��
�������F��C�غ�ʱ��FG=FP=CK����ʱFG��ֵ���
��t=$\frac{11}{2}$sʱ��FG��ֵ���
��3������ͼ2�У�����AI��IQ��ID��
����I��AC��AB����ʱ����IAD=��IAC=15�㣬��IQD=30�㣬
���QAI=��QIA=15�㣬
��AQ=IQ����ID=x����IQ=AQ=2x��DQ=$\sqrt{3}$x��
��AD=2$\sqrt{3}$��
��2x+$\sqrt{3}$x=2$\sqrt{3}$��
��x=4$\sqrt{3}$-6��
��DQ=$\sqrt{3}$x=12-6$\sqrt{3}$��
��t=$\frac{12-6\sqrt{3}}{\sqrt{3}}$=4$\sqrt{3}$-6��
��ͼ3�У���t��2ʱ����I��AC��AB����ʱ��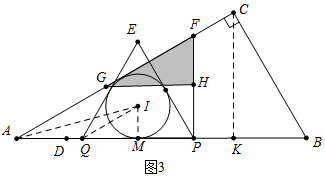
��֪PQ=4$\sqrt{3}$����IM��PQ��M��
��֪QM=2$\sqrt{3}$��IM=2��AQ=QI=4��
��DQ=AQ-AD=4-2$\sqrt{3}$��
��DP=DQ+QP=4+2$\sqrt{3}$��
��t=$\frac{4+2\sqrt{3}}{\sqrt{3}}$=$\frac{4\sqrt{3}+6}{3}$��
��ͼ4�У���P��B�غ�ʱ����I��AB��BC���У���ʱt=$\frac{8\sqrt{3}}{\sqrt{3}}$=8��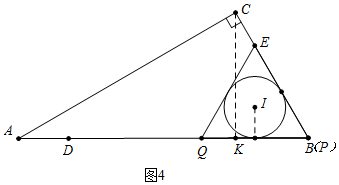
������������t=��4$\sqrt{3}$-6��s��$\frac{4\sqrt{3}+6}{3}$s��8sʱ����I���ABC���������У�
����ͼ5�У�����G�ڡ�I��ʱ����ʱ��֪AQ=QG=QD=$\sqrt{3}$��t=1s��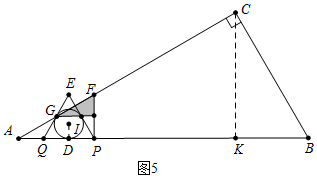
��ͼ6�У���t��2ʱ����G�ڡ�I��ʱ����֪DG=EG=AD=2$\sqrt{3}$����ʱ��Q��D�غϣ�t=$\frac{4\sqrt{3}}{\sqrt{3}}$=4��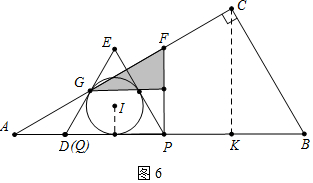
�ɴ˿�֪����1��t��4ʱ����G�ڡ�I�ڣ�
��ͼ7�У�����G�ڡ�I��ʱ����GK��PQ��K��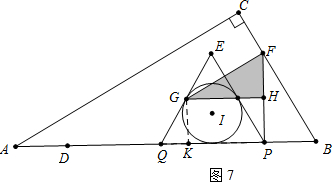
��֪PF=2PH=2GK=6��
��Rt��PFB�У���PF=6����B=60�㣬
��PB=$\frac{PF}{\sqrt{3}}$=2$\sqrt{3}$��
��DP=6$\sqrt{3}$��
��t=6��
��ͼ8�У�����G�ڡ�I��ʱ����֪��PFGʱ�ȱ������Σ�PF=PG=FG=2��PB=$\frac{2}{\sqrt{3}}$=$\frac{2}{3}$$\sqrt{3}$��
��PD=8$\sqrt{3}$-$\frac{2}{3}$$\sqrt{3}$=$\frac{22\sqrt{3}}{3}$��
��t=$\frac{22}{3}$��
�ɴ˿�֪��6��t��$\frac{22}{3}$ʱ����G�ڡ�I�ϣ�
������������1��t��4��6��t��$\frac{22}{3}$ʱ����G�ڡ�I�ڣ�
���� ���⿼��Բ�ۺ��⡢�ȱ������ε����ʡ�ֱ��������30�Ƚ����ʡ�ƽ�Ʊ任��ֱ����Բ��������������Բλ�ù�ϵ��֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬ѧ��ȡ����λ�ý��ʵ�����⣬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �� | �� | �� | |
| ƽ���������صĶ�������֣� | 10 | 5 | 7.5 |
| ƽ��ÿ�ֻ���ɻ����磨��Ԫ�� | 5 | 3.6 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
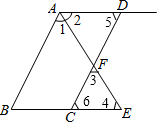 ��ͼ��AB��CD��AEƽ�֡�BAD��CD��AE�ཻ��F����3=��4����֤����5=��6��
��ͼ��AB��CD��AEƽ�֡�BAD��CD��AE�ཻ��F����3=��4����֤����5=��6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
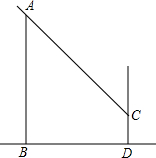 ��ͼ��һλͬѧ��������Ӱ��������AB���ĸ߶ȣ�����ijһʱ�̲�ø�Ϊ1�����ֱ��ʱӰ��Ϊ0.9�ף���ʱ����������һ�������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ����Ӱ��������ǽ��CD���������Ȳ������ǽ�ϵ�Ӱ�ӣ�CD����Ϊ1.2�ף��ֲ�õ��沿�ֵ�Ӱ����BD��Ϊ2.7�ף�������õ�����ӦΪ�����ף�
��ͼ��һλͬѧ��������Ӱ��������AB���ĸ߶ȣ�����ijһʱ�̲�ø�Ϊ1�����ֱ��ʱӰ��Ϊ0.9�ף���ʱ����������һ�������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ����Ӱ��������ǽ��CD���������Ȳ������ǽ�ϵ�Ӱ�ӣ�CD����Ϊ1.2�ף��ֲ�õ��沿�ֵ�Ӱ����BD��Ϊ2.7�ף�������õ�����ӦΪ�����ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
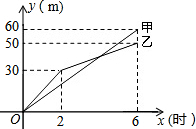 ij����һ������ʩ���У������γ�����ȵ����е��������ֱ��ס�������ʩ����ͬʱ����ʩ������ͼ�Ƿ�ӳ���������е��ij���y���ף���ʩ��ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺
ij����һ������ʩ���У������γ�����ȵ����е��������ֱ��ס�������ʩ����ͬʱ����ʩ������ͼ�Ƿ�ӳ���������е��ij���y���ף���ʩ��ʱ��x��ʱ��֮���ϵ�IJ���ͼ�������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
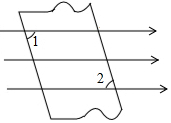 ��ͼ��һ��ƽ�й����в���һ�ŶԱ�ƽ�е�ֽ�壬��������ֽ�����Ϸ����ɵġ�=65��25�䣬��ô������ֽ�����·����ɵġ�2�Ķ�����65��25�䣮
��ͼ��һ��ƽ�й����в���һ�ŶԱ�ƽ�е�ֽ�壬��������ֽ�����Ϸ����ɵġ�=65��25�䣬��ô������ֽ�����·����ɵġ�2�Ķ�����65��25�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com