

分析 (1)先证明△ADE∽△FBE,利用相似的性质得BF;
(2)①利用相似三角形的判定,证明Rt△F′HN∽Rt△F′EG,利用相似三角形的性质,求得HN,利用三角形的面积公式得结果;②利用相似三角形的判定,证明Rt△F′HN∽Rt△F′EG,利用相似三角形的性质,求得HN,利用三角形的面积公式得结果.
解答 解:(1)∵BE=AB=15,
在直角△BCE中,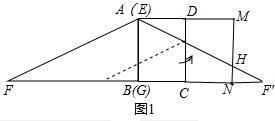
CE=$\sqrt{{BE}^{2}{-BC}^{2}}$=$\sqrt{{15}^{2}{-12}^{2}}$=9
∴DE=6,
∵∠EAD+∠BAE=90°,∠BAE=∠BEF,
∴∠EAD+∠BEF=90°,
∵∠BEF+∠F=90°,
∴∠EAD=∠F
∵∠ADE=∠FBE
∴△ADE∽△FBE,
∴$\frac{AD}{BF}=\frac{DE}{BE}$,
$\frac{12}{BF}=\frac{6}{15}$,
∴BF=30;
(2)①如图1,将矩形ABCD和直角△FBE以CD为轴翻折,则△AMH即为未包裹住的面积,
∵Rt△F′HN∽Rt△F′EG,
∴$\frac{F′N}{F′G}$=$\frac{HN}{EG}$,即$\frac{6}{30}=\frac{HN}{15}$,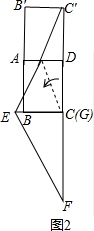
解得:HN=3,
∴S△AMH=$\frac{1}{2}$•AM•MH=$\frac{1}{2}$×12×24=144;
②如图2,将矩形ABCD和Rt△ECF以AD为轴翻折,
∵Rt△GBE∽Rt△GB′C′,
∴$\frac{GB}{GB′}=\frac{EB}{B′C′}$,即$\frac{30-GB′}{GB′}=\frac{3}{12}$,解得:GB′=24,
∴S△B′C′G=$\frac{1}{2}$•B′C′•B′G=$\frac{1}{2}$×12×24=144,
∴按照两种包裹方法的未包裹面积相等.
点评 本题主要考查了相似三角形的判定和性质及翻折变化,以动态(平移和旋转)的形式考查了分类讨论的思想、函数的知识和直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:
已知△A1B1C1是由△ABC经过平移得到的,其中,A、B、C三点的对应点分别是A1、B1、C1,它们在平面直角坐标系中的坐标如下表所示:| △ABC | A(a,0) | B(3,0) | C(5,5) |
| △A1B1C1 | A1(-3,2) | B1(-1,b) | C1(c,7) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
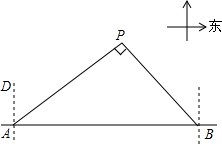 钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.
钓鱼岛自古以来就是中国的领土,如图,我国甲、乙两艘海岛执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往P处海域巡查的任务,并测得P处位于A处北偏东53.5°方向上、在B的西北方向上,船B在船A正东方向140海里处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
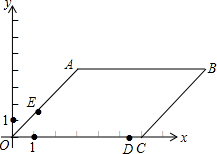 如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com