
分析 过点A作AE∥CD,交BC于点E,可得出四边形ADCE是平行四边形,再根据等腰梯形的性质及平行线的性质得出∠AEB=∠BCD=60°,由三角形外角的定义求出∠EAC的度数,故可得出四边形ADEC是菱形,再由等边三角形的判定定理得出△ABE是等边三角形,由此可得出结论.
解答 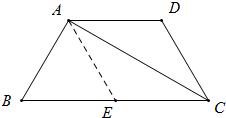 解:过点A作AE∥CD,交BC于点E,
解:过点A作AE∥CD,交BC于点E,
∵梯形ABCD是等腰梯形,∠B=60°,
∴AD∥BC,
∴四边形ADCE是平行四边形,
∴∠AEB=∠BCD=60°,
∵CA平分∠BCD,
∴∠ACE=$\frac{1}{2}$∠BCD=30°,
∵∠AEB是△ACE的外角,
∴∠AEB=∠ACE+∠EAC,即60°=30°+∠EAC,
∴∠EAC=30°,
∴AE=CE=3,
∴四边形ADEC是菱形,
∵△ABE中,∠B=∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=AE=3,
∴梯形ABCD的周长=AB+(BE+CE)+CD+AD=3+3+3+3+3=15.
故答案为:15.
点评 本题考查的是等腰梯形的性质,根据题意作出辅助线,构造出平行四边形是解答此题的关键.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
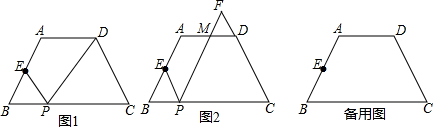
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2015)2+2016 | B. | y=(x-2015)2+2016 | C. | y=-(x-2015)2-2016 | D. | y=-(x+2015)2+2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
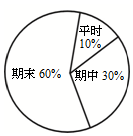 小明同学八年级上学期的数学成绩记录如表:
小明同学八年级上学期的数学成绩记录如表:| 测验类别 | 平时测验 | 期中考试 | 期末考试 | |||
| 测验1 | 测验2 | 测验3 | 课题学习 | |||
| 成绩 | 88 | 72 | 86 | 98 | 90 | 84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com