
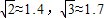 ).
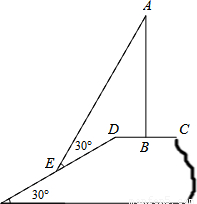
).
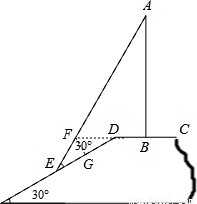 解:延长BD交AE于点F,作FG⊥ED于点G,
解:延长BD交AE于点F,作FG⊥ED于点G, ED=9米,
ED=9米,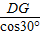 =
=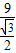 =6
=6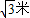 ,
,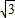 +6)米,
+6)米,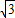 +6)×
+6)×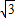 =(18+6
=(18+6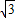 )≈28.2米,
)≈28.2米,

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
 (2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(
(2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:解答题
在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高(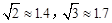 ).
).

查看答案和解析>>
科目:初中数学 来源:抚顺 题型:解答题
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com