
分析 根据分式的减法和除法可以化简题目中的式子,然后在-2≤x<2中选取一个使得原分式有意义的整数代入化简后的式子即可解答本题.
解答 解:($\frac{2x+1}{1-x}$-1)÷$\frac{x}{1-{x}^{2}}$
=$\frac{2x+1-(1-x)}{1-x}•\frac{(1+x)(1-x)}{x}$
=$\frac{2x+1-1+x}{1-x}•\frac{(1+x)(1-x)}{x}$
=$\frac{3x}{1-x}•\frac{(1+x)(1-x)}{x}$
=3(1+x)
=3+3x,
∵-2≤x<2且x为整数,
∴当x=-2时,原式=3+3×(-2)=3+(-6)=-3.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.


科目:初中数学 来源: 题型:选择题
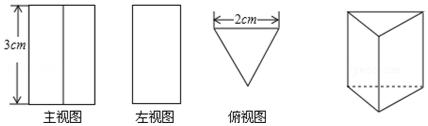
| A. | 18cm2 | B. | 20cm2 | C. | (18+2$\sqrt{3}$)cm2 | D. | (18+4$\sqrt{3}$)cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
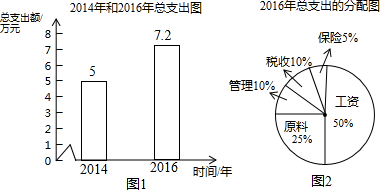
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
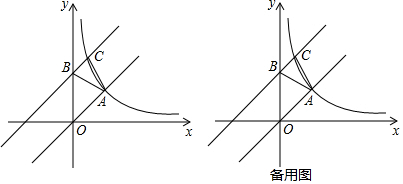
 如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )
如图,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2017C2017,则m的值和点C2017的坐标是( )| A. | 2,(-22017,22017×$\sqrt{3}$) | B. | 2,(-22018,0) | ||
| C. | $\sqrt{3}$,(-22017,22017×$\sqrt{3}$) | D. | $\sqrt{3}$,(-22018,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
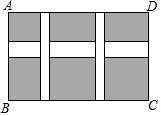 如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.
如图,某小区规划在一个长40米,宽36米的矩形场地ABCD上修建横、纵道路宽为3:2的三条道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为198平方米,求道路的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com