
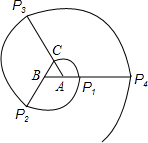
 如图,正△ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4,….设ln为扇形Dn的弧长(n=1,2,3,…),Sn为扇形Dn的面积.
如图,正△ABC的边长为1cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3绕点A顺时针旋转120°至AP4,形成扇形D4,….设ln为扇形Dn的弧长(n=1,2,3,…),Sn为扇形Dn的面积.| n | 1 | 2 | 3 | 4 | 5 | … |
| ln |
| 120π×1 |
| 180 |
| 2π |
| 3 |
| 120π×2 |
| 180 |
| 4π |
| 3 |
| 120π×3 |
| 180 |
| 120π×4 |
| 180 |
| 8π |
| 3 |
| 120π×5 |
| 180 |
| 10π |
| 3 |
| 120nπ |
| 180 |
| 2nπ |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
| 8π |
| 3 |
| 10π |
| 3 |
| 2nπ |
| 3 |
| 2nπ |
| 3 |
| 120π×12 |
| 360 |
| π |
| 3 |
| 120π×22 |
| 360 |
| 22π |
| 3 |
| 120π×32 |
| 360 |
| 32π |
| 3 |
| n2π |
| 3 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
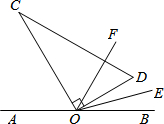 如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度.
如图,点O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.已知∠AOC的度数比∠BOD的度数的3倍多10度.查看答案和解析>>
科目:初中数学 来源: 题型:
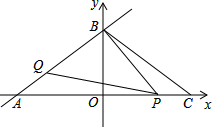 如图,直线l:y=
如图,直线l:y=| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
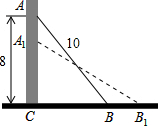 如果一个长为10m的梯子AB,斜靠在墙上,梯子的顶端距地面的垂直距离AC为8m.如果梯子的顶端A下滑1m到A1,请猜测梯子底端B滑动的1距离是否也会是1m?若不是,请求出滑动的距离.
如果一个长为10m的梯子AB,斜靠在墙上,梯子的顶端距地面的垂直距离AC为8m.如果梯子的顶端A下滑1m到A1,请猜测梯子底端B滑动的1距离是否也会是1m?若不是,请求出滑动的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com