
分析 档次提高时,带来每件利润的提高,销售量下降,设生产第x档次时获得产品的利润为y元,每件利润为[8+2(x-1)]元,销售量为[800-40(x-1)]件,根据:利润=每件利润×销售量列函数式,化成顶点式即可.
解答 解:设生产第x档次时获得产品的利润为y元,则
∵生产最低档次产品每件获利润8元,每提高一个档次,每件利润增加2元.用同样工时每天可生产最低档次产品800件,每提高一个档次将减产40件,
∴y=[8+2(x-1)][800-40(x-1)]=-80(x-9)2+11520,
∵当x=9时,y有最大值,
所以,生产第九档次产品获利润最大.
点评 本题考查二次函数的实际应用,借助二次函数解决实际问题,解题的关键是能够从实际问题中抽象出二次函数模型,难度不大.


科目:初中数学 来源: 题型:解答题
 已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
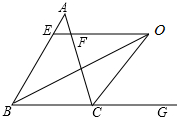 如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.
如图,在△ABC中,∠ABC的平分线与△ABC的外角平分线交于点O,过O作BC的平行线交AB于E,交AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空
如图所示,直线CD同侧有两个点A,B,在CD上找一点P使得AP+BP最短,并说明理由,盼盼的解题思路如下,请你帮助完成操作及填空查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2a}{c}=\frac{d}{b}$ | B. | $\frac{a}{c}=\frac{d}{2b}$ | C. | $\frac{2a}{d}=\frac{c}{b}$ | D. | $\frac{a}{2c}=\frac{d}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com