
 如图,在平行四边形ABCD中,AB=5,BC=10,BC边上的高为4,动点P从点B出发,以每秒1个单位的速度沿线段BA运动到点A后,再以每秒1个单位的速度沿线段AD运动,到点D停止.当点P不与平行四边形的顶点重合时,过点P作P所在边的垂线PQ交直线BC于点Q,以PQ为一边作正方形PQMN,使点N落在射线PA或PD上,设点P运动时间为t秒,正方形PQMN与平行四边形ABCD重叠部分的面积为S(平方单位).
如图,在平行四边形ABCD中,AB=5,BC=10,BC边上的高为4,动点P从点B出发,以每秒1个单位的速度沿线段BA运动到点A后,再以每秒1个单位的速度沿线段AD运动,到点D停止.当点P不与平行四边形的顶点重合时,过点P作P所在边的垂线PQ交直线BC于点Q,以PQ为一边作正方形PQMN,使点N落在射线PA或PD上,设点P运动时间为t秒,正方形PQMN与平行四边形ABCD重叠部分的面积为S(平方单位).分析 (1)分两种情况进行计算,当P在AB或AD上时,根据正方形的性质和∠B的正切进行计算即可;
(2)根据四边形ABQM是平行四边形,得MQ=AB=5,利用tan∠B=$\frac{PQ}{BP}$=$\frac{4}{3}$,求t的值;
(3)先计算当N与A重合时,如图5,t=$\frac{15}{7}$,
再分三种情况讨论:①当0<t≤$\frac{15}{7}$时,正方形PQMN与平行四边形ABCD重叠部分是正方形PQMN,
②当$\frac{15}{7}$$<t≤\frac{15}{4}$时,如图6,此时正方形PQMN与平行四边形ABCD重叠部分是五边形APQME,
③当$\frac{15}{4}$<t<15时,如图7此时正方形PQMN与平行四边形ABCD重叠部分是梯形APQE,
分别求出重叠部分面积;
(4)点F在正方形PQMN的边PN上时,有两个时间段,分别计算F从D到A运动、从A返回到D时,当F分别与P与N重合时的两个分界线即可.
解答  解:(1)如图1,过A作AE⊥BC于E,
解:(1)如图1,过A作AE⊥BC于E,
∵AB=5,AE=4,
∴BE=3,
∴tan∠B=$\frac{AE}{BE}=\frac{4}{3}$,
当0<t<5时,如图2,由题意得:BP=t,
在Rt△BPQ中,tan∠B=$\frac{PQ}{BP}$,
∴$\frac{PQ}{t}$=$\frac{4}{3}$,
∴PQ=$\frac{4t}{3}$,
∵四边形PQMN是正方形,
∴QM=PQ=$\frac{4t}{3}$;
当5<t<15时,如图3,
∵四边形PQMN是正方形,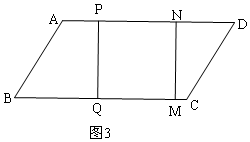
∴PQ⊥AD,
∵BC边上的高为4,
∴PQ=QM=4,
综上所述,QM的长为$\frac{4t}{3}$或4;
(2)当点M落在线段AD上时,如图4,
∵四边形PQMN是正方形,
∴PN∥QM,
∴AB∥QM,
∵AM∥BQ,
∴四边形ABQM是平行四边形,
∴MQ=AB=5,
∴PQ=5,
tan∠B=$\frac{PQ}{BP}$=$\frac{4}{3}$,
∴$\frac{5}{t}=\frac{4}{3}$,
∴t=$\frac{15}{4}$;
(3)当N与A重合时,如图5,
∵BP=t,PN=PQ=$\frac{4t}{3}$,
由BP+PN=AB=5得:t+$\frac{4t}{3}$=5,
t=$\frac{15}{7}$,
①当0<t≤$\frac{15}{7}$时,正方形PQMN与平行四边形ABCD重叠部分是正方形PQMN,
∴S=QM2=$(\frac{4t}{3})^{2}$=$\frac{16{t}^{2}}{9}$,
②当$\frac{15}{7}$$<t≤\frac{15}{4}$时,如图6,
此时正方形PQMN与平行四边形ABCD重叠部分是五边形APQME,
∵BP=t,AB=5,
∴PA=5-t,
∵PN=$\frac{4t}{3}$,
∴AN=$\frac{4t}{3}$-(5-t)=$\frac{7t}{3}$-5,
∵tan∠NAE=tan∠B,
∴$\frac{NE}{AN}=\frac{4}{3}$,
∴NE=$\frac{4}{3}$AN=$\frac{4}{3}$($\frac{7t}{3}$-5)=$\frac{28t}{9}$-$\frac{20}{3}$,
∴S=S正方形NPQM-S△ANE=$(\frac{4t}{3})^{2}$-$\frac{1}{2}$($\frac{7t}{3}$-5)($\frac{28t}{9}$-$\frac{20}{3}$)=-$\frac{50}{27}{t}^{2}+\frac{140}{9}t-\frac{50}{3}$;
③当$\frac{15}{4}$<t<15时,如图7,
此时正方形PQMN与平行四边形ABCD重叠部分是梯形APQE,
∵AP=5-t,EQ=5,PQ=$\frac{4t}{3}$,
∴S=S梯形APQE=$\frac{1}{2}$(AP+EQ)•PQ,
=$\frac{1}{2}$(5-t+5)×$\frac{4t}{3}$,
=-$\frac{2}{3}{t}^{2}$+$\frac{20}{3}t$;
综上所述,S与t的函数关系式为:
S=$\left\{\begin{array}{l}{\frac{16}{9}{t}^{2}(0<t≤\frac{15}{7})}\\{-\frac{50}{27}{t}^{2}+\frac{140}{9}t-\frac{50}{3}(\frac{15}{7}<t≤\frac{15}{4})}\\{-\frac{2}{3}{t}^{2}+\frac{20}{3}t(\frac{15}{4}<t<15)}\end{array}\right.$,
(4)设F运动时间为t′秒,
如图8,BP′=4,P在边AD上运动时,当F与N重合时,
AP=t′-1,DF=5t′,PN=4,
由AP+PN+DN=10得:t′-1+4+5t′=10,
t′=$\frac{7}{6}$;
t=$\frac{7}{6}+4$═$\frac{31}{6}$
当F与P第一次重合时,如图9,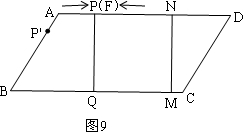
由AP+DF=10得:t′-1+5t′=10,
t′=$\frac{11}{6}$,
t=$\frac{11}{6}$+4=$\frac{35}{6}$,
∴点F从D到A运动时,在正方形PQMN的边PN上时t的取值范围是$\frac{31}{6}$≤t$≤\frac{35}{6}$;
当F与P第二次重合时,如图10,
此时PD=FD=20-5t′,AP=t′-1,
由AP+DF=10得:20-5t′+t′-1=10,
t′=$\frac{9}{4}$,
∴t=$\frac{9}{4}$+4=$\frac{25}{4}$,
当F最后回到终点D时,t′=4,
当F与N第二次重合时,如图11,
FD=20-5t′,AP=t′-1,
由AP+PN+FD=10得:t′-1+4+20-5t′=10,
t′=$\frac{13}{4}$<4,
∴t=$\frac{13}{4}$+4=$\frac{29}{4}$,
∴点F从A到D运动时,在正方形PQMN的边PN上时t的取值范围是$\frac{25}{4}$≤t$≤\frac{29}{4}$;
综上所述,在正方形PQMN的边PN上时t的取值范围是$\frac{31}{6}$≤t$≤\frac{35}{6}$和$\frac{25}{4}$≤t$≤\frac{29}{4}$.
点评 本题是四边形的综合题,考查了平行四边形的性质、正方形的性质和判定、动点运动问题,以及重叠部分面积的求法,比较复杂,解决两个问题是关键:①根据图形正确表示点P的路程,②第四问中注意F的路线是:D-A-D,时间是4秒后,F开始运动.


科目:初中数学 来源: 题型:解答题
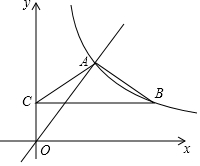 如图,函数y=$\frac{4}{3}$x与函数y=$\frac{m}{x}$(x>0)的图象相交于点A(n,4).点B在函数y=$\frac{m}{x}$(x>0)的图象上,过点B作BC∥x轴,BC与y轴相交于点C,且AB=AC.
如图,函数y=$\frac{4}{3}$x与函数y=$\frac{m}{x}$(x>0)的图象相交于点A(n,4).点B在函数y=$\frac{m}{x}$(x>0)的图象上,过点B作BC∥x轴,BC与y轴相交于点C,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).
如图,直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,已知二次函数的图象经过点A、C和点B(-1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com