
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
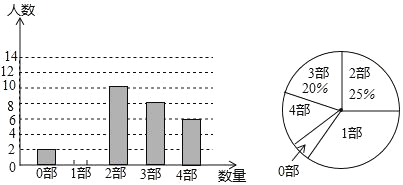
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是____部,中位数是_____部;
(2)扇形统计图中“4部”所在扇形的圆心角为_____度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
【答案】(1)1、2;(2)54;(3)补图见解析;(4)![]() .
.
【解析】
(1)先根据调查的总人数,求得1部对应的人数,进而得到本次调查所得数据的众数以及中位数;
(2)根据扇形圆心角的度数=部分占总体的百分比×360°,即可得到“4部”所在扇形的圆心角;
(3)根据1部对应的人数为40﹣2﹣10﹣8﹣6=14,即可将条形统计图补充完整;
(4)根据树状图所得的结果,判断他们选中同一名著的概率.
解:(1)∵调查的总人数为:10÷25%=40,
∴1部对应的人数为40﹣2﹣10﹣8﹣6=14,
∴本次调查所得数据的众数是1部,
∵2+14+10=26>21,2+14<20,
∴中位数为2部,
故答案为:1、2;
(2)扇形统计图中“4部”所在扇形的圆心角为:![]() ×360°=54°;
×360°=54°;
故答案为:54;
(3)条形统计图如图所示,
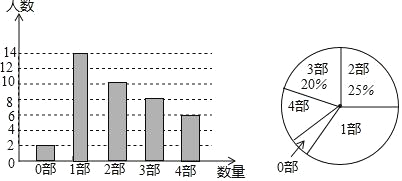
(4)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,
画树状图可得:
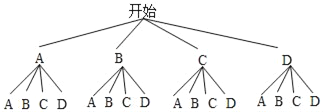
共有16种等可能的结果,其中选中同一名著的有4种,
故P(两人选中同一名著)=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线![]() 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C(![]() ,0)作CD交AB于D,交
,0)作CD交AB于D,交![]() 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.

(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,并体现绿色节能理念,我市某工厂降低了某种工艺品的成本,两个月内从每件产品成本50元,降低到了每件32元,
(1)请问工厂平均每月降低率为多少?
(2)该工厂将产品投放市场进行实销,经过调查,得到如下数据:
销售单价 | …… | 40 | 50 | 60 | 70 | …… |
每天销售量 | …… | 400 | 300 | 200 | 100 | …… |
把上表中![]() 、
、![]() 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想![]() 与
与![]() 的函数关系,并求出函数关系式.
的函数关系,并求出函数关系式.
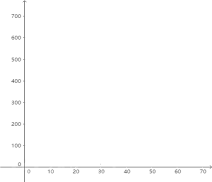
(3)当销售单价定为多少时,工艺厂试销该工艺品每天活得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
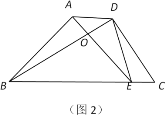
【题目】如图1,在四边形ABCD中,∠BAD=∠BDC=90°,AB=AD,∠DCB=60°,CD=8.
(1)若P是BD上一点,且PA=CD,求∠PAB的度数.
(2)①将图1中的△ABD绕点B顺时针旋转30°,点D落在边BC上的E处,AE交BD于点O,连接DE,如图2,求证:DE2=DODB;
②将图1中△ABD绕点B旋转α得到△A'BD'(A与A',D与D'是对应点),若CD'=CD,则cosα的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①函数![]() 的自变量
的自变量![]() 的取值范围是
的取值范围是![]() ;②对角线相等的四边形是矩形;③正六边形的中心角为
;②对角线相等的四边形是矩形;③正六边形的中心角为![]() ;④对角线互相平分且相等的四边形是菱形;⑤计算
;④对角线互相平分且相等的四边形是菱形;⑤计算![]() 的结果为7:⑥相等的圆心角所对的弧相等;⑦
的结果为7:⑥相等的圆心角所对的弧相等;⑦![]() 的运算结果是无理数.其中正确的个数有( )
的运算结果是无理数.其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
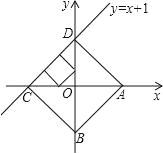
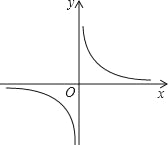
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
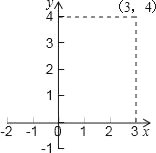
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:![]() 、
、![]() 都是关于
都是关于![]() 的多项式,
的多项式,![]() ,
,![]() ,其中多项式
,其中多项式![]() 有一项被“□”遮挡住了.
有一项被“□”遮挡住了.
(1)当![]() 时,
时,![]() ,请求出多项式
,请求出多项式![]() 被“□”遮挡的这一项的系数;
被“□”遮挡的这一项的系数;
(2)若![]() 是单项式,请直接写出多项式
是单项式,请直接写出多项式![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com