
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式. 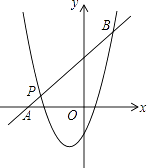
(3)直接写出y1>y2时x的取值范围.
【答案】
(1)解:∵对称轴是经过(﹣1,0)且平行于y轴的直线,
∴﹣ ![]() =﹣1,
=﹣1,
∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(﹣3,1),
∴9﹣3m+n=1,
∴n=3m﹣8=﹣2
(2)解:∵m=2,n=﹣2,
∴二次函数为y=x2+2x﹣2,
作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,
∴ ![]() =
= ![]() ,
,
∵P(﹣3,1),
∴PC=1,
∵PA:PB=1:5,
∴PA:AB=1:6,
∴BD=6,
∴B的纵坐标为6,
代入二次函数为y=x2+2x﹣2得,6=x2+2x﹣2,
解得x1=2,x2=﹣4(舍去),
∴B(2,6),
则 ![]() ,
,
解得, ![]() ,
,
∴一次函数的表达式为y2=x+4
(3)解:由图象可知,当x<﹣3或x>2时,y1>y2.

【解析】(1)利用对称轴公式求得m,把P(﹣3,1)代入二次函数y=x2+mx+n得出n=3m﹣8,进而就可求得n;(2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得B的纵坐标,代入二次函数的解析式中求得B的坐标,然后利用待定系数法就可求得一次函数的表达式;(3)结合图形解答即可.


科目:初中数学 来源: 题型:
【题目】2017年中考,阜阳市某区计划在4月中旬的某个周二至周四这3天进行理化加试.王老师和朱老师都将被邀请当监考老师,王老师随机选择2天,朱老师随机选择1天当监考老师.
(1)求王老师选择周二、周三这两天的概率是多少?
(2)求王老师和朱老师两人同一天监考理化加试的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.三角形的内心到三角形三条边的距离相等
B.三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等
C.对于实数a,b,若|a|≤|b|,则a≤b
D.对于实数x,若 ![]() =x,则x≥0
=x,则x≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】准备一张矩形纸片,按如图操作: 将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.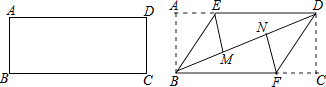
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,边AO在Y轴上,点B1、B2、B3…都在直线y= ![]() x上,则点A2016的坐标为( )
x上,则点A2016的坐标为( )
A.(2016 ![]() ,2018)
,2018)
B.(2016 ![]() ,2016)
,2016)
C.(2016,2016 ![]() )
)
D.(2016,2018 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(﹣8,0),点B的坐标为(﹣8,6),直线BC∥x轴,交y轴于点C,将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于点P、Q.
(1)四边形OABC的形状是 , 当α=90°时, ![]() 的值是 .
的值是 .
(2)①如图2,当四边形OA′B′C′的顶点B′落在y轴正半轴上时,求 ![]() 的值;
的值;
②如图3,当四边形OA′B′C′的顶点B′落在BC的延长线上时,求△OPB′的面积.

(3)在四边形OABC旋转过程中,当0°<α≤180°时,是否存在这样的点P和点Q,使BP= ![]() BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
BQ?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,分别以B、C为圆心,BC长为半径在BC下方画弧.设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD
(1)求证:AD平分∠BAC。
(2)若BC=6,∠BAC=50°,求弧DE、弧DF的长度之和。(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上
(1)求斜坡AB的水平宽度BC。
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高。(![]() ≈2.236,结果精确到0.1m)
≈2.236,结果精确到0.1m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com