
证明:平行四边形的对角线的平方之和等于各边的平方之和.
已知:如图,在平行四边形ABCD中,AC和BD是对角线.
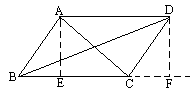
求证:AC2+BD2=AB2+BC2+CD2+DA2.
|
证明:过A作AE⊥BC于E,过D作DF⊥BC于F. ∵AB=CD,AE=DF,(作垂直构造直角) ∴Rt△ABE≌Rt△DCF,∴BE=CF. ∵AC2=(BC-BE)2+AE2=BC2-2BC·BF+BE2+AE2 =BC2+BE2-2BC·BE+AB2-BE2 =BC2+AB2-2BC·BE, 而BD2=(BC+CF)2+DF2=BC2+2BC·CF+CF2+DC2-CF2 =BC2+CD2+2BC·BE,(用上全等得到边的转化) ∴AC2+BD2=BC2+AB2-2BC·BE+BC2+CD2+2BC·BE =AB2+BC2+CD2+DA2. 分析:从所求证算式的结构上看,平方和的形式容易联想到勾股定理,因此首先要想办法构造直角三角形. |
|
注:本题的易错点是不先写已知求证,解题的关键是做出辅助线构造直角三角形运用勾股定理. |


科目:初中数学 来源: 题型:阅读理解


查看答案和解析>>
科目:初中数学 来源: 题型:
 在下面推理过程的括号内填上推理的依据
在下面推理过程的括号内填上推理的依据| ∥ | . |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省昆明三中、滇池中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,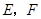 是平行四边形
是平行四边形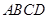 的对角线
的对角线 上的点,
上的点, .请你猜想:
.请你猜想: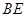 与
与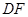 有怎样的位置关系和数量关系?并对你的猜想加以证明:
有怎样的位置关系和数量关系?并对你的猜想加以证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com