
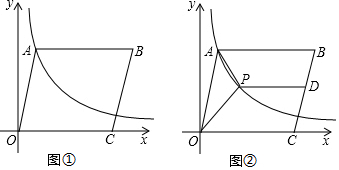
分析 (1)由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数关系式,再根据平行四边形的性质结合点A、O、C的坐标即可求出点B的坐标;
(2)延长DP交OA于点E,由点D为线段BC的中点,可求出点D的坐标,再令反比例函数关系式中y=2求出x值即可得出点P的坐标,由此即可得出PD、EP的长度,根据三角形的面积公式即可得出结论.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$(x>0)的图象经过点A(1,4).
∴m=1×4=4,
∴反比例函数的关系式为y=$\frac{4}{x}$(x>0).
∵四边形OABC为平行四边形,且点O(0,0),OC=5,点A(1,4),
∴点C(5,0),
∴点B(6,4).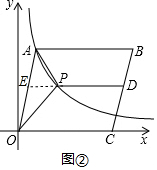 (2)延长DP交OA于点E,如图②所示.
(2)延长DP交OA于点E,如图②所示.
∵点D为线段BC的中点,点C(5,0)、B(6,4),
∴点D($\frac{11}{2}$,2).
令y=$\frac{4}{x}$中y=2,则x=2,
∴点P(2,2),
∴PD=$\frac{11}{2}$-2=$\frac{7}{2}$,EP=ED-PD=$\frac{3}{2}$,
∴S△AOP=$\frac{1}{2}$EP•(yA-yO)=$\frac{1}{2}$×$\frac{3}{2}$×(4-0)=3.
点评 本题考查了反比例函数图象上点的坐标特征、三角形的面积公式、平行四边形的性质,解题的关键是:根据反比例函数图象上点的坐标特征求出反比例函数解析式.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | C. | $\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{2}{3}$ | D. | $\sqrt{{2}^{3}}$=3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 15 | 20 | 25 |
| 千克(千克) | 30 | 40 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20.12×102 | B. | 0.2012×104 | C. | 2.012×103 | D. | 2.012×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
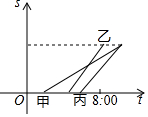 甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )
甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如图所示.那么8:00时,距A城最远的汽车是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 甲车和乙车 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com