
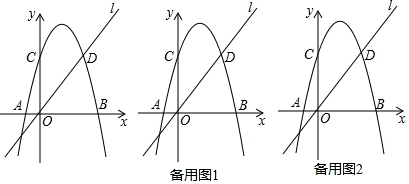
���� ��1����C��D���꣬���ô���ϵ��������������߽���ʽ��
��2���ٿ�����������ߵĶԳ����ֱ��l�Ľ���ʽ��������E�����꣬��������֤��TE��x�ᣬ������T�������꣬���������߽���ʽ�������T�����ꣻ�ڹ�E��BP��ƽ���ߣ���y���ڵ�F����x���ڵ�H������ƽ���߷��߶γɱ��������OF=OE�������F�����꣬������ֱ��EF�Ľ���ʽ��������ֱ��PB�Ľ���ʽ����B���������ֱ��PB����ʽ�������P�����꣮
��� �⣺
��1����C��D�����������������߽���ʽ�ɵ�$\left\{\begin{array}{l}{c=8}\\{36a+18+c=8}\end{array}\right.$�����$\left\{\begin{array}{l}{c=8}\\{a=-\frac{1}{2}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{1}{2}$x2+3x+8��
��2���١�y=-$\frac{1}{2}$x2+3x+8=-$\frac{1}{2}$��x-3��2+$\frac{25}{2}$��
�������߶Գ���Ϊx=3��
��ֱ��l����ʽΪy=kx��
��D��6��8������ɵ�8=6k�����k=$\frac{3}{4}$��
��ֱ��l�Ľ���ʽΪy=$\frac{4}{3}$x��
��E��3��4����
��O��0��0����C��0��8����
��OE=CE��
���E���߶�OC�Ĵ�ֱƽ�����ϣ�
�ߡ�TEC=��TEO��
��TE��x�ᣬ
��T��������Ϊ4��
��y=-$\frac{1}{2}$x2+3x+8�У���y=4�ɵ�4=-$\frac{1}{2}$x2+3x+8�����x=3+$\sqrt{17}$��x=3-$\sqrt{17}$��
��T��������3+$\sqrt{17}$��4����3-$\sqrt{17}$��4����
����y=-$\frac{1}{2}$x2+3x+8�У���y=0�ɵ�0=-$\frac{1}{2}$x2+3x+8�����x=-2��x=8��
��B��8��0����
��E��3��4����
��OE=5��
��ͼ2������E��BP��ƽ���ߣ���y���ڵ�F����x���ڵ�H��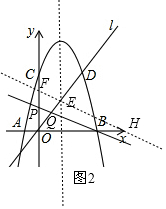
��$\frac{OP}{OF}$=$\frac{OQ}{OE}$��
��OP=OQ��
��OF=OE=5��
��F��0��5����
�����ֱ��PB�Ľ���ʽΪy=kx+5��
��E���������ɵ�4=3k+5�����k=-$\frac{1}{3}$��
��ֱ��EF�Ľ���ʽΪy=-$\frac{1}{3}$x+5��
�����ֱ��PB�Ľ���ʽΪy=-$\frac{1}{3}$x+m��
��B���������ɵ�0=-$\frac{1}{3}$��8+m�����m=$\frac{8}{3}$��
��P��������0��$\frac{8}{3}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ƽ���ߵ����ʡ�ƽ���߷��߶γɱ�����֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2���������E����������ǽ���Ĺؼ����ڢ������F��������ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �õ������ȣ� | 140 | 160 | 180 | 200 |
| ���� | 1 | 3 | 4 | 2 |
| A�� | 180��180 | B�� | 180��160 | C�� | 160��180 | D�� | 160��160 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
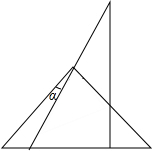
 ��ͼ����ABC�У�BF��CF�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ�DF��BC��AC��E������ABC���ܳ�Ϊ15��BC=4�����ADE���ܳ�Ϊ��������
��ͼ����ABC�У�BF��CF�ֱ��ǡ�ABC�͡�ACB��ƽ���ߣ�DF��BC��AC��E������ABC���ܳ�Ϊ15��BC=4�����ADE���ܳ�Ϊ��������| A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 һ�����ǰ���ͼ������һ����ͼ�СϦ��Ķ���Ϊ��������
һ�����ǰ���ͼ������һ����ͼ�СϦ��Ķ���Ϊ��������| A�� | 35�� | B�� | 30�� | C�� | 25�� | D�� | 15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{a}{-a-b}$ | B�� | -$\frac{a}{a+b}$ | C�� | $\frac{a}{a+b}$ | D�� | -$\frac{a}{a-b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
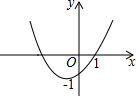 ��ͼ��������y=ax2+bx+c��a��0�����㣨1��0���͵㣨0��-1�����Ҷ����ڵ������ޣ���a��ȡֵ��Χ�ǣ�������
��ͼ��������y=ax2+bx+c��a��0�����㣨1��0���͵㣨0��-1�����Ҷ����ڵ������ޣ���a��ȡֵ��Χ�ǣ�������| A�� | a��0 | B�� | 0��a��1 | C�� | 1��a��2 | D�� | -1��a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-6y=xy | B�� | 3x-6=x | C�� | 3x-$\frac{6}{y}$=0 | D�� | 3x-6y=x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 1�·��̳���װ�������۶���22��Ԫ | |
| B�� | 3�·��̳���װ�������۶��2�·ݼ����� | |
| C�� | 4�·��̳�����Ʒ���۶���75��Ԫ | |
| D�� | 5�·��̳���װ�������۶��4�·ݼ����� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com